
| A. | 1 | B. | $\frac{3}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
分析 根据题意列出相应的表格,得到所有等可能出现的情况数,进而找出满足题意的情况数,即可求出所求的概率.
解答 解:列表如下:
| 1 | 2 | 3 | 4 | |
| 1 | --- | (2,1) | (3,1) | (4,1) |
| 2 | (1,2) | --- | (3,2) | (4,2) |
| 3 | (1,3) | (2,3) | --- | (4,3) |
| 4 | (1,4) | (2,4) | (3,4) | --- |
点评 此题考查了列表法与树状图法,以及中心对称图形,用到的知识点为:概率=所求情况数与总情况数之比.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
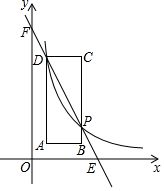 如图,矩形ABCD中,点A(1,1)、B(3,1),C(3,6),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,且与BC交于点P.
如图,矩形ABCD中,点A(1,1)、B(3,1),C(3,6),反比例函数y=$\frac{m}{x}$(x>0)的图象经过点D,且与BC交于点P.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 6 | D. | 2$\sqrt{7}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
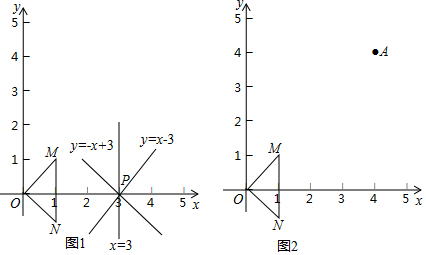
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x1=0,x2=4 | B. | x1=-2,x2=6 | C. | x1=$\frac{3}{2}$,x2=$\frac{5}{2}$ | D. | x1=-4,x2=0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
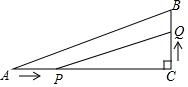 如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )
如图,在Rt△ABC中,∠C=90°,AC=6cm,BC=2cm,点P在边AC上,从点A向点C移动,点Q在边CB上,从点C向点B移动.若点P,Q均以1cm/s的速度同时出发,且当一点移动到终点时,另一点也随之停止,连接PQ,则线段PQ的最小值是( )| A. | 20cm | B. | 18cm | C. | 2$\sqrt{5}$cm | D. | 3$\sqrt{2}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
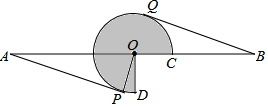 如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.
如图,AB=16,O为AB中点,点C在线段OB上(不与点O,B重合),将OC绕点O逆时针旋转270°后得到扇形COD,AP,BQ分别切优弧$\widehat{CD}$于点P,Q,且点P,Q在AB异侧,连接OP.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com