
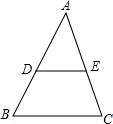
 如图,△ABC,DE∥BC,若S△ADE:S梯形DBCE=9:16,那么AD:DB=3:2.
如图,△ABC,DE∥BC,若S△ADE:S梯形DBCE=9:16,那么AD:DB=3:2. 分析 由S△ADE:S梯形DBCE=9:16,且△ADE和梯形DBCE的面积之和等于△ABC的面积,所以△ADE的面积与△ABC的面积之比为9:25,然后由DE∥BC,得出△ADE与△ABC相似,根据相似三角形的面积比等于相似比的平方,求出对应边AD与AB的比,根据比例性质即可求出AD:DB的比值.
解答 解:∵S△ADE:S梯形DBCE=9:16,
∴S△ADE:S△ABC=9:25,
又∵DE∥BC,
∴△ADE∽△ABC,
∴S△ADE:S△ABC=(AD:AB)2,
∴AD:AB=3:5,
∴AD:DB=3:2.
故答案为3:2.
点评 此题考查了相似三角形的判定与性质,要求学生掌握两三角形相似时,对应边之比等于相似比;周长比等于相似比;对应量(除面积)之比等于相似比;面积之比等于相似比的平方.此题的关键是利用面积之比求出相似比即对应边之比,这种方法称为“列比例式求解法”.同时考查了比例的性质.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
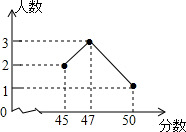 在2015年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数分别是( )
在2015年的体育中考中,某校6名学生的体育成绩统计如图,则这组数据的众数、中位数分别是( )| A. | 3,2.5 | B. | 47,46 | C. | 47,47 | D. | 50,47 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
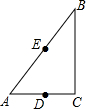 如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是AC、AB的中点.若作半径为8的⊙B,则下列选项中的点在⊙B内的是( )
如图,在△ABC中,∠C=90°,AC=6,BC=8,D、E分别是AC、AB的中点.若作半径为8的⊙B,则下列选项中的点在⊙B内的是( )| A. | 点A | B. | 点D | C. | 点C | D. | 点E |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,线段AB的长为4,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作得等腰直角三角形ACD和等腰直角三角形BCE,
已知如图,线段AB的长为4,C为AB上的一个动点,分别以AC、BC为斜边在AB的同侧作得等腰直角三角形ACD和等腰直角三角形BCE,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
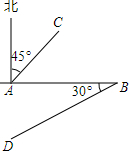 如图,是某油田的四口油井的位置图,图中1cm表示实际距离1.5km.请你仔细观察,并量一量图中的距离,用语言叙述这四口油井之间的位置关系.
如图,是某油田的四口油井的位置图,图中1cm表示实际距离1.5km.请你仔细观察,并量一量图中的距离,用语言叙述这四口油井之间的位置关系.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com