
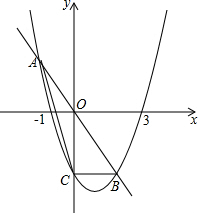
 已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.
已知抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,与y轴交于点C,直线y=kx与抛物线交于A,B两点.分析 (1)令抛物线解析式中x=0求出y值即可得出C点的坐标,有点(-1,0)、(3,0)利用待定系数法即可求出抛物线的解析式;
(2)将正比例函数解析式代入抛物线解析式中,找出关于x的一元二次方程,根据根与系数的关系即可得出“xA+xB=2+k,xA•xB=-3”,结合点O为线段AB的中点即可得出xA+xB=2+k=0,由此得出k的值,将k的值代入一元二次方程中求出xA、xB,在代入一次函数解析式中即可得出点A、B的坐标;
(3)假设存在,利用三角形的面积公式以及(2)中得到的“xA+xB=2+k,xA•xB=-3”,即可得出关于k的一元二次方程,结合方程无解即可得出假设不成了,从而得出不存在满足题意的k值.
解答 解:(1)令抛物线y=ax2+bx-3中x=0,则y=-3,
∴点C的坐标为(0,-3).
∵抛物线y=ax2+bx-3经过(-1,0),(3,0)两点,
∴有$\left\{\begin{array}{l}{0=a-b-3}\\{0=9a+3b-3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=-2}\end{array}\right.$,
∴此抛物线的解析式为y=x2-2x-3.
(2)将y=kx代入y=x2-2x-3中得:kx=x2-2x-3,
整理得:x2-(2+k)x-3=0,
∴xA+xB=2+k,xA•xB=-3.
∵原点O为线段AB的中点,
∴xA+xB=2+k=0,
解得:k=-2.
当k=-2时,x2-(2+k)x-3=x2-3=0,
解得:xA=-$\sqrt{3}$,xB=$\sqrt{3}$.
∴yA=-2xA=2$\sqrt{3}$,yB=-2xB=-2$\sqrt{3}$.
故当原点O为线段AB的中点时,k的值为-2,点A的坐标为(-$\sqrt{3}$,2$\sqrt{3}$),点B的坐标为($\sqrt{3}$,-2$\sqrt{3}$).
(3)假设存在.
由(2)可知:xA+xB=2+k,xA•xB=-3,
S△ABC=$\frac{1}{2}$OC•|xA-xB|=$\frac{1}{2}$×3×$\sqrt{({x}_{A}+{x}_{B})^{2}-4{x}_{A}•{x}_{B}}$=$\frac{3\sqrt{10}}{2}$,
∴(2+k)2-4×(-3)=10,即(2+k)2+2=0.
∵(2+k)2非负,无解.
故假设不成立.
所以不存在实数k使得△ABC的面积为$\frac{3\sqrt{10}}{2}$.
点评 本题考查了待定系数法求函数解析式、根与系数的关系、解一元二次方程以及三角形的面积公式,解题的关键是:(1)利用待定系数法求出函数解析式;(2)结合根与系数的关系求出k值;(3)利用反正法找出方程无解.本题属于中档题,难度不大,解决该题型题目时,将正比例函数解析式代入二次函数解析式中,利用三角形的面积公式结合根与系数的关系找出关于k的方程是关键.


 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:选择题
| A. | -2或4 | B. | 2或-4 | C. | 4或-6 | D. | -4或6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 小组 | 研究报告 | 小组展示 | 答辩 |
| 甲 | 91 | 80 | 78 |
| 乙 | 81 | 74 | 85 |
| 丙 | 79 | 83 | 90 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
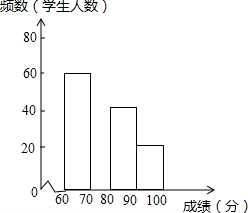 在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:
在2016CCTV英语风采大赛中,娄底市参赛选手表现突出,成绩均不低于60分.为了更好地了解娄底赛区的成绩分布情况,随机抽取了其中200名学生的成绩(成绩x取整数,总分100分)作为样本进行了整理,得到如图的两幅不完整的统计图表:| 成绩 | 频数 | 频率 |
| 60≤x<70 | 60 | 0.30 |
| 70≤x<80 | m | 0.40 |
| 80≤x<90 | 40 | n |
| 90≤x≤100 | 20 | 0.10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=5,b=1 | B. | a=-5,b=1 | C. | a=5,b=-1 | D. | a=-5,b=-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
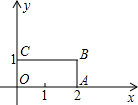 如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1),C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA1B1C1,B为对应点为B1,且B1在OB的延长线上,则B1的坐标为(4,2).
如图,在平面直角坐标系中,矩形OABC的顶点坐标分别为O(0,0),A(2,0),B(2,1),C(0,1),以坐标原点O为位似中心,将矩形OABC放大为原图形的2倍,记所得矩形为OA1B1C1,B为对应点为B1,且B1在OB的延长线上,则B1的坐标为(4,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com