
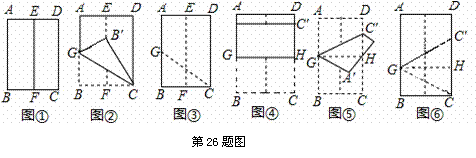
如图所示,将矩形纸片ABC![]() D按如下顺序进行折叠:对折,展平,得折痕EF(如图①);沿CG折叠,使点B落在EF上的点B′处,(如图②);展平,得折痕GC(如图③);沿GH折叠,使点C落在DH上的点C′处,(如图④);沿GC′折叠(如图
D按如下顺序进行折叠:对折,展平,得折痕EF(如图①);沿CG折叠,使点B落在EF上的点B′处,(如图②);展平,得折痕GC(如图③);沿GH折叠,使点C落在DH上的点C′处,(如图④);沿GC′折叠(如图
⑤);展平,得折痕GC′,GH(如图 ⑥).
(1)求图 ②中∠BCB′的大小.
(2)图⑥中的△GCC![]() ′是正三角形吗?请说明理由.
′是正三角形吗?请说明理由.
![]()
分析:(1)由折叠的性质知:=BC,然后在Rt△中,求得cos∠的值,利用特殊角的三角函数值的知识即可求得∠BCB′的度数;
(2)首先根据题意得:GC平分∠BCB′,即可求得∠GCC′的度数,然后由折叠的性质知:GH是线段CC′的对称轴,可得GC′=GC,即可得△GCC′是正三角形.
解:(1)由折叠的性质知: =BC,
在Rt△中,∵ cos∠=,∴ ∠=60°,即∠BCB′=60°.
(2)根据题意得:GC平分∠BCB′,∴ ∠GCB=∠GCB′=∠BCB′=30°,
∴ ∠GCC′=∠BCD-∠BCG=60°.
由折叠的性质知:GH是线段CC′的对称轴,∴ GC′=GC,∴ △GCC′是正三角形.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

| A、60° | B、67.5° | C、72° | D、75° |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
(2011•广州)如图所示,将矩形纸片先沿虚线AB按箭头方向向右对折,接着对折后的纸片沿虚线CD向下对折,然后剪下一个小三角形,再将纸片打开,则打开后的展开图是( )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com