
【题目】在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
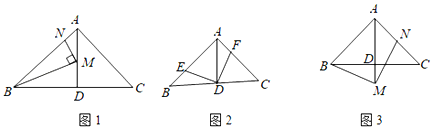
(1)如图1,点M,N分别在AD,AB上,且∠BMN=90°,当∠AMN=30°,AB=2时,求线段AM的长;
(2)如图2,点E,F分别在AB,AC上,且∠EDF=90°,求证:BE=AF;
(3)如图3,点M在AD的延长线上,点N在AC上,且∠BMN=90°,求证:AB+AN=![]() AM.
AM.
【答案】(1)![]() ﹣
﹣![]() ;(2)证明见解析;(3)见解析
;(2)证明见解析;(3)见解析
【解析】
(1)根据等腰三角形的性质、直角三角形的性质得到AD=BD=DC=![]() ,求出∠MBD=30°,根据勾股定理计算即可;
,求出∠MBD=30°,根据勾股定理计算即可;
(2)证明△BDE≌△ADF,根据全等三角形的性质证明;
(3)过点M作ME∥BC交AB的延长线于E,证明△BME≌△AMN,根据全等三角形的性质得到BE=AN,根据等腰直角三角形的性质、勾股定理证明结论.
解:(1)∵∠BAC=90°,AB=AC,AD⊥BC,
∴AD=BD=DC,∠ABC=∠ACB=45°,∠BAD=∠CAD=45°,
∵AB=2,
∴AD=BD=DC=![]() ,
,
∵∠AMN=30°,
∴∠BMD=180°﹣90°﹣30°=60°,
∴∠MBD=30°,
∴BM=2DM,
由勾股定理得,BM2﹣DM2=BD2,即(2DM)2﹣DM2=(![]() )2,
)2,
解得,DM=![]() ,
,
∴AM=AD﹣DM=![]() ﹣
﹣![]() ;
;
(2)∵AD⊥BC,∠EDF=90°,
∴∠BDE=∠ADF,
在△BDE和△ADF中

∴△BDE≌△ADF(ASA)
∴BE=AF;
(3)过点M作ME∥BC交AB的延长线于E,

∴∠AME=90°,
则AE=![]() AM,∠E=45°,
AM,∠E=45°,
∴ME=MA,
∵∠AME=90°,∠BMN=90°,
∴∠BME=∠AMN,
在△BME和△NMA中
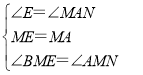
∴△BME≌△AMN(ASA),
∴BE=AN,
∴AB+AN=AB+BE=AE=![]() AM.
AM.


科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,点D在AB上,以AD为直径的⊙O与BC相
交于点E,且AE平分∠BAC.
(1)求证:BC是⊙O的切线;
(2)若∠EAB=30°,OD=3,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,点P为AD上一个动点,以PB 为对称轴将△APB折叠得到△EPB,点A的对称点为点E,射线BE交矩形ABCD的边于点 F,若AB=4,AD=6,当点F为矩形ABCD边的中点时,AP的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着生活质量的提高,人们健康意识逐渐增强,安装净水设备的百姓家庭越来越多.某厂家从去年开始投入生产净水器,生产净水器的总量y(台)与今年的生产天数x(天)的关系如图所示.今年生产90天后,厂家改进了技术,平均每天的生产数量达到30台.
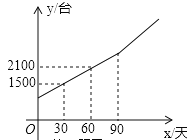
(1)求y与x之间的函数表达式;
(2)已知该厂家去年平均每天的生产数量与今年前90天平均每天的生产数量相同,求厂家去年生产的天数;
(3)如果厂家制定总量不少于6000台的生产计划,那么在改进技术后,至少还要多少天完成生产计划?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区调查社区居民双休日的学习状况,采取下列调查方式:①从一幢高层住宅楼中选取200名居民;②从不同住层楼中随机选取200名居民;③选取社区内的200名在校学生.
(1)上述调查方式最合理的是 (填序号);
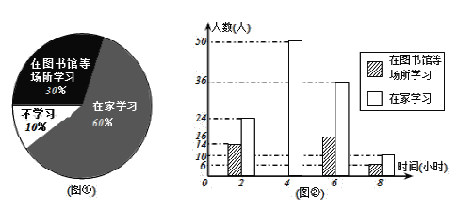
(2)将最合理的调查方式得到的数据制成扇形统计图(如图①)和频数分布直方图(如图②).
①请补全直方图(直接画在图②中);
②在这次调查中,200名居民中,在家学习的有 人;
(3)请估计该社区2000名居民中双休日学习时间不少于4h的人数;
(4)小明的叔叔住在该社区,那么双休日他去叔叔家时,正好叔叔没有学习的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
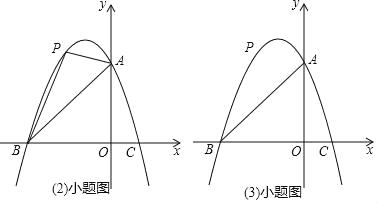
【题目】已知:如图,抛物线y=ax2+bx+3与坐标轴分别交于点A,B(﹣3,0),C(1,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线解析式;
(2)当点P运动到什么位置时,△PAB的面积最大?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P作PE∥x轴交抛物线于点E,连接DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求点P的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2-2![]() mx+m2+m-1(m为常数).
mx+m2+m-1(m为常数).
(1)求证:不论m为何值,该二次函数的图像与x轴总有两个公共点;
(2)将该二次函数的图像向下平移k(k>0)个单位长度,使得平移后的图像经过点(0,-2),则k的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要求在下列问题中仅用无刻度的直尺作图.如图,在下列10×12的网格中, 横、纵坐标均为整数的点叫做格点.例如正方形ABCD的顶点A(0,7),C(5,2)都是格点.
(1)找一个格点M, 连接AM交边CD于F,使DF=FC,画出图形写出点M的坐标为 ;
(2)找一个格点N, 连接ON交边BC于E,使BE=![]() BC,画出图形写出点N的坐标为 ;
BC,画出图形写出点N的坐标为 ;
(3)连接AE、EF得△AEF.请按步骤完成作图,并写出△AEF的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在矩形纸片![]() 中,
中,![]() ,
,![]() ,折叠纸片使
,折叠纸片使![]() 点落在边
点落在边![]() 上的
上的![]() 处,拆痕为
处,拆痕为![]() .过点
.过点![]() 作
作![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
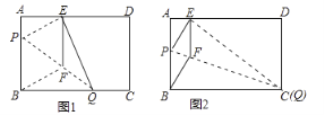
(1)求证:四边形![]() 为菱形;
为菱形;
(2)当点![]() 在
在![]() 边上移动时,折痕的端点
边上移动时,折痕的端点![]() 、
、![]() 也随之移动;
也随之移动;
①当点![]() 与点
与点![]() 重合时(如图2),求菱形
重合时(如图2),求菱形![]() 的边长;
的边长;
②若限定![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上移动,求
上移动,求![]() 的内切圆半径的取值范围.
的内切圆半径的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com