
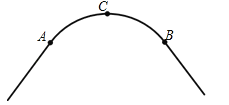
【题目】如图,一条公路的转弯处是一段圆弧(![]() ).
).
(1)用直尺和圆规作出![]() 所在圆的圆心O;(要求保留作图痕迹,不写作法)
所在圆的圆心O;(要求保留作图痕迹,不写作法)
(2)若![]() 的中点C到弦AB的距离为20m,AB=80m,求
的中点C到弦AB的距离为20m,AB=80m,求![]() 所在圆的半径.
所在圆的半径.
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
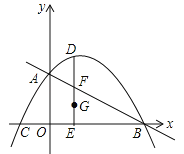
【题目】如图,抛物线![]() 与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
与坐标轴交于A、B、C三点,其中B(4,0)、C(﹣2,0),连接AB、AC,在第一象限内的抛物线上有一动点D,过D作DE⊥x轴,垂足为E,交AB于点F.
(1)求此抛物线的解析式;
(2)在DE上作点G,使G点与D点关于F点对称,以G为圆心,GD为半径作圆,当⊙G与其中一条坐标轴相切时,求G点的横坐标;
(3)过D点作直线DH∥AC交AB于H,当△DHF的面积最大时,在抛物线和直线AB上分别取M、N两点,并使D、H、M、N四点组成平行四边形,请你直接写出符合要求的M、N两点的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的为( )
A.购买一张彩票,中奖
B.通常加热到100℃时,水沸腾
C.任意画一个三角形,其内角和是360°
D.射击运动员射击一次,命中靶心
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 两条对角线互相平分的四边形是平行四边形
B. 两条对角线互相垂直的四边形是菱形
C. 两条对角线互相垂直且相等的四边形是正方形
D. 两条对角线相等的四边形是矩形
查看答案和解析>>
科目:初中数学 来源: 题型:
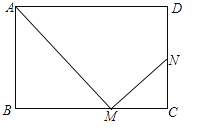
【题目】在矩形ABCD中,AB=a,AD=b,点M为BC边上一动点(点M与点B、C不重合),连接AM,过点M作MN⊥AM,垂足为M,MN交CD或CD的延长线于点N.
(1)求证:△CMN∽△BAM;
(2)设BM=x,CN=y,求y关于x的函数解析式.当x取何值时,y有最大值,并求出y的最大值;
(3)当点M在BC上运动时,求使得下列两个条件都成立的b的取值范围:①点N始终在线段CD上,②点M在某一位置时,点N恰好与点D重合.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=8,点E,F分别在AB,AD上,且AE=AF,过点E作EG∥AD交CD于点G,过点F作FH∥AB交BC于点H,EG与FH交于点O.当四边形AEOF与四边形CGOH的周长之差为12时,AE的值为( ) 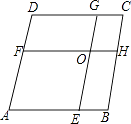
A.6.5
B.6
C.5.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着城际铁路的正式开通,从甲市经丙市到乙市的高铁里程比普快里程缩短了90km,运行时间减少了8h,已知甲市到乙市的普快列车里程为1220km.高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王先生要从甲市去距离大约780km的丙市参加14:00召开的会议,如果他买到当日9:20从甲市到丙市的高铁票,而且从丙市火车站到会议地点最多需要1小时.试问在高铁列车准点到达的情况下,它能否在开会之前20分钟赶到会议地点?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com