
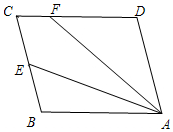
 如图,平行四边形ABCD中,E是BC边的中点,连接AE、F为CD边上一点,且满足∠DFA=2∠BAE.
如图,平行四边形ABCD中,E是BC边的中点,连接AE、F为CD边上一点,且满足∠DFA=2∠BAE.分析 (1)根据平行四边形的性质、平行线的性质证得∠DFA=∠FAB=40°;然后结合已知条件∠DFA=2∠BAE求得∠FAE=∠BAE,从而求得∠FAE的度数;
(2)在AF上截取AG=AB,连接EG,CG.利用全等三角形的判定定理SAS证得△AEG≌△AEB,由全等三角形的对应角相等、对应边相等知EG=BE,∠B=∠AGE;然后由中点E的性质平行线的性质以及等腰三角形的判定与性质求得CF=FG;最后根据线段间的和差关系证得结论.
解答 (1)解:∵∠D=110°,∠DAF=25°,
∴∠DFA=180°-∠D-∠DAF=45°(三角形内角和定理).
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD(平行四边形对边平行且相等).
∴∠DFA=∠FAB=45°(两直线平行,内错角相等);
∵∠DFA=2∠BAE(已知),
∴∠FAB=2∠BAE(等量代换).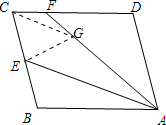
即∠FAE+∠BAE=2∠BAE.
∴∠FAE=∠BAE;
∴2∠FAE=45°,
∴∠FAE=22.5°;
(2)证明:在AF上截取AG=AB,连接EG,CG.
∵∠FAE=∠BAE,AE=AE,
∴△AEG≌△AEB.
∴EG=BE,∠B=∠AGE;
又∵E为BC中点,
∴CE=BE.
∴EG=EC,
∴∠EGC=∠ECG;
∵AB∥CD,
∴∠B+∠BCD=180°.
又∵∠AGE+∠EGF=180°,∠AGE=∠B,
∴∠BCF=∠EGF;
又∵∠EGC=∠ECG,
∴∠FGC=∠FCG,
∴FG=FC;
又∵AG=AB,AB=CD,
∴AF=AG+GF=AB+FC=CD+FC.
点评 本题考查了平行四边形的性质、全等三角形的判定与性质.利用平行四边形的性质,可以证角相等、线段相等.其关键是根据所要证明的全等三角形,选择需要的边、角相等条件.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:解答题
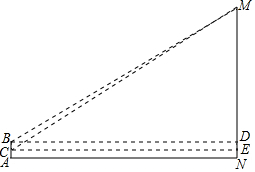 某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着侧倾器和皮尺来测量这个距离.测量方法如下:如图,首先,小军站在“聚贤亭”的A处,用侧倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米,然后,小军在A处蹲下,用侧倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为1米.请你利用以上测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果精确到1米).(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245,sin24°≈0.4067,cos24°≈0.9135,tan24°≈0.4452.)
某市一湖的湖心岛有一棵百年古树,当地人称它为“乡思柳”,不乘船不易到达,每年初春时节,人们喜欢在“聚贤亭”观湖赏柳.小红和小军很想知道“聚贤亭”与“乡思柳”之间的大致距离,于是,有一天,他们俩带着侧倾器和皮尺来测量这个距离.测量方法如下:如图,首先,小军站在“聚贤亭”的A处,用侧倾器测得“乡思柳”顶端M点的仰角为23°,此时测得小军的眼睛距地面的高度AB为1.7米,然后,小军在A处蹲下,用侧倾器测得“乡思柳”顶端M点的仰角为24°,这时测得小军的眼睛距地面的高度AC为1米.请你利用以上测得的数据,计算“聚贤亭”与“乡思柳”之间的距离AN的长(结果精确到1米).(参考数据:sin23°≈0.3907,cos23°≈0.9205,tan23°≈0.4245,sin24°≈0.4067,cos24°≈0.9135,tan24°≈0.4452.)查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,一次函数y=kx+2k(k>0)的图象交x轴于点A,P为该一次函数在第一象限内图象上一点,点C(m,n)与点P关于y轴对称,且满足n-m=6,若△APC是直角三角形,则k的值为1.
如图,一次函数y=kx+2k(k>0)的图象交x轴于点A,P为该一次函数在第一象限内图象上一点,点C(m,n)与点P关于y轴对称,且满足n-m=6,若△APC是直角三角形,则k的值为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
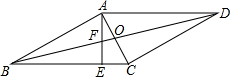 如图,在平行四边形ABCD中,对角线AC、BD交于点O、AC⊥AB、∠ABC=30°,过点A作AE⊥BC于点E,交BD于点F,则$\frac{AF}{AO}$=$\frac{4\sqrt{3}}{7}$.
如图,在平行四边形ABCD中,对角线AC、BD交于点O、AC⊥AB、∠ABC=30°,过点A作AE⊥BC于点E,交BD于点F,则$\frac{AF}{AO}$=$\frac{4\sqrt{3}}{7}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
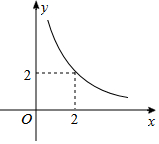 设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )
设△ABC的一边长为x,这条边上的高为y,y与x满足的反比例函数关系如图所示.当△ABC为等腰直角三角形时,x+y的值为( )| A. | 4 | B. | 5 | C. | 5或3$\sqrt{2}$ | D. | 4或3$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -2a+2b=-2(a+b) | B. | a2-2a+4=(a-2)2 | C. | (2a2)3=6a6 | D. | 3a2•2a3=6a5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com