
在下列性质中,平行四边形不一定具有的是
[ ]
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
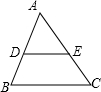 在八年级上册我们已经知道三角形的中位线具有如下性质:
在八年级上册我们已经知道三角形的中位线具有如下性质:| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:伴你学数学 八年级 上册 题型:044
在下列性质中,平行四边形具有的是________,矩形具有的是________,菱形具有的是________,正方形具有的是________.
(1)四条边都相等
(2)对角线互相平分
(3)对角线相等
(4)对角线互相垂直
(5)四个角都是直角
(6)每一条对角线平分一组对角
(7)对边相等且平行
(8)有两条对称轴
(将相应性质的序号填在相应的横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2011年安徽省马鞍山市成功学校中考数学一模试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com