
【题目】在△ABC中,AB=AC,∠A=60°,点D是线段BC的中点,∠EDF=120°,DE与线段AB相交于点E,DF与线段AC(或AC的延长线)相交于点F.
(1)如图(1)所示,若DF⊥AC,垂足为F,AB=4,求BE的长;
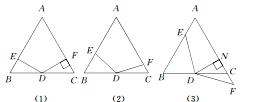
(2)如图(2)所示,将(1)中的∠EDF绕点D顺时针旋转一定的角度,DF仍与线段AC相交于点F,求证:BE+CF=![]() AB;
AB;
(3)如图(3)所示,将(2)中的∠EDF继续绕点D顺时针旋转一定的角度,使DF与线段AC的延长线交于点F,作DN⊥AC于点N,若DN=FN,求证:BE+CF=![]() (BE-CF).
(BE-CF).
【答案】(1)BE=1;(2)详见解析;(3)详见解析.
【解析】试题分析:(1)根据四边形的内角和定理得出DE⊥AB,从而得到BE的长度;
(2)取AB得中点G,连接DG,得出DG为△ABC的中位线,则DG=DC,∠BGD=∠C=60°,根据四边形对角互补得出∠GED=∠DFC,从而得到△DEG≌△DFC,得到BG=CF,得出答案;
(3)取AB得中点G,连接DG,同(2),易证△DEG≌△DFC,得出EG=CF,设CN=x,根据Rt△DCN得出CD=2x,DN=![]() x,根据题意得出EG、BE与x的关系,从而进行证明.
x,根据题意得出EG、BE与x的关系,从而进行证明.
试题解析:(1)由四边形AEDF的内角和为360°,可知DE⊥AB,故BE=2
(2)取AB的中点G,连接DG
易证:DG为△ABC的中位线,故DG=DC,∠BGD=∠C=60°
又四边形AEDF的对角互补,故∠GED=∠DFC
∴△DEG≌△DFC
故EG=CF
∴BE+CF=BE+EG=BG=![]() AB
AB
(3)取AB的中点G,连接DG
同(2),易证△DEG≌△DFC
故EG=CF
故BE-CF=BE-EG=BG=![]() AB
AB
设CN=x
在Rt△DCN中,CD=2x,DN=![]() x
x
在RT△DFN中,NF=DN=![]() x,故EG=CF=(
x,故EG=CF=(![]() -1)x
-1)x
BE=BG+EG=DC+CF=2x+(![]() -1)x=(
-1)x=(![]() +1)x
+1)x
故BE+CF=(![]() +1)x+(
+1)x+(![]() -1)x=2
-1)x=2![]() x
x
![]() (BE-CF)=
(BE-CF)=![]() [(
[(![]() +1)x-(
+1)x-(![]() -1)]=2
-1)]=2![]() x
x
故BE+CF=![]() (BE-CF)
(BE-CF)


科目:初中数学 来源: 题型:
【题目】下列式子满足完全平方公式的是()
A.(3x﹣y)(﹣y﹣3x)
B.(3x﹣y)(3x+y)
C.(﹣3x﹣y)(y﹣3x)
D.(﹣3x﹣y)(y+3x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】x轴将坐标平面分为两部分,x轴上方的点的纵坐标为正数,x轴下方的点的纵坐标为______;y轴把坐标平面分为两部分,y轴左侧的点的横坐标为_____,y轴右侧的点的横坐标为_____.规定原点坐标是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=96°,D是BC延长线上的一点,∠ABC与∠ACD(△ACB的外角)的平分线交于A1点,则∠A1=_______度;如果∠A=α,按以上的方法依次作出∠BA2C,∠BA3C…∠BAnC(n为正整数),则∠An=_______度(用含α的代数式表示).
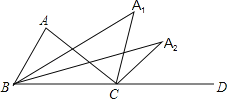
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,AE、BF分别平分∠DAB和∠ABC,交CD于点E、F,AE、BF相交于点M.
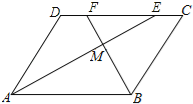
(1)试说明:AE⊥BF;
(2)判断线段DF与CE的大小关系,并予以说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定两数a,b之间的一种运算,记作(a,b):如果![]()
![]() ,那么(a,b)=c.
,那么(a,b)=c.
例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,填空:
(3,27)=_______,(5,1)=_______,(2,![]()
![]() )=_______.
)=_______.
(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:
设(3n,4n)=x,则(3n)x=4n,即(3x)n=4n
所以3x=4,即(3,4)=x,
所以(3n,4n)=(3,4).
请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com