
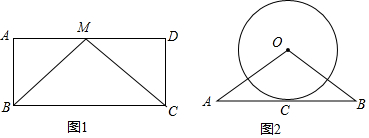
分析 (1)根据矩形的性质可得出∠A=∠D、AB=DC,根据M为边AD的中点可得出AM=DM,再利用全等三角形的判定定理SAS即可证出△ABM≌△DCM;
(2)连接OC,根据切线的性质可得出OC⊥AB,由AO=BO利用等腰三角形的性质即可得出AC=8,在Rt△AOC中利用勾股定理即可求出OA的长度.
解答 (1)证明:∵四边形ABCD为矩形,
∴∠A=∠D,AB=DC.
∵M为边AD的中点,
∴AM=DM.
在△ABM和△DCM中,$\left\{\begin{array}{l}{AB=DC}\\{∠A=∠D}\\{AM=DM}\end{array}\right.$,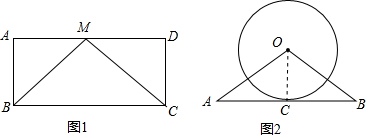
∴△ABM≌△DCM(SAS).
(2)解:在图2中,连接OC.
∵AB与⊙O相切于C,
∴OC⊥AB.
∵AO=BO,
∴AC=$\frac{1}{2}$AB=8.
在Rt△AOC中,∠ACO=90°,OC=6,AC=8,
∴OA=$\sqrt{O{C}^{2}+A{C}^{2}}$=10.
点评 本题考查了切线的性质、矩形的性质、全等三角形的判定、等腰三角形的性质以及勾股定理,解题的关键是:(1)利用全等三角形的判定定理SAS证出△ABM≌△DCM;(2)构建合适的直角三角形,利用勾股定理求出OA的长度.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,铁路上A,B两点相距20km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=10km,CB=5km,现在要在铁路AB上建一个货运站E,使得C,D两村到E站距离相等,问:E站应建立在离A多少千米处?
如图,铁路上A,B两点相距20km,C,D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=10km,CB=5km,现在要在铁路AB上建一个货运站E,使得C,D两村到E站距离相等,问:E站应建立在离A多少千米处?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
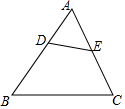 如图所示,D、E分别是△ABC的边AB、AC上的点,试添加一个条件:∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}=\frac{AE}{AB}$.使得△ABC∽△AED.
如图所示,D、E分别是△ABC的边AB、AC上的点,试添加一个条件:∠ADE=∠C或∠AED=∠B或$\frac{AD}{AC}=\frac{AE}{AB}$.使得△ABC∽△AED.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 请你根据学函数这一章所获得的学习经验来探究.
请你根据学函数这一章所获得的学习经验来探究.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com