
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)在图1中,∠AOC= °,∠MOC= °;
(2)将图1中的三角板按图2的位置放置,使得OM在射线QA上,求∠CON的度数;
(3)将上述直角三角板按图3的位置放置,OM在∠BOC的内部,说明∠BON﹣∠COM的值固定不变.

【答案】(1)120,150;(2)30°;(3)30°.
【解析】
(1)点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,可以求得∠AOC和∠MOC的度数;
(2)根据∠AOC的度数和∠MON的度数可以得到∠CON的度数;
(3)根据∠BOC=60°,∠MON=90°,∠BON=∠MON﹣∠BOM,∠COM=∠BOC﹣∠BOM,可以得到∠BON﹣∠COM的度数.
解:(1)∵点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,∠AOC+∠BOC=180°,
∴∠AOC=120°,∠BOC=60°,
∵∠BOM=90°,
∴∠MOC=150°,
故答案为:120,150;
(2)∵由(1)可知:∠AOC=120°,∠MON=90°,∠AOC=∠MON+∠CON,
∴∠CON=∠AOC﹣∠MON=120°﹣90°=30°;
(3)由图可知:∠BOC=60°,∠MON=90°,∠BON=∠MON﹣∠BOM,∠COM=∠BOC﹣∠BOM,
则,∠BON﹣∠COM=90°﹣∠BOM﹣(60°﹣∠BOM)=30°,
即∠BON﹣∠COM的度数是30°.


科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.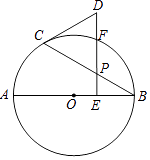
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑到学校.如果小明跑步的速度均匀的,到达小彬家用了8分钟,整个跑步过程用时共32分钟.
(1)以小明家为原点、向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家;
(2)用点C表示出学校的位置;
(3)求小彬家与学校之间的距离.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请根据图中提供的信息,回答下列问题

(1)一个暖瓶与一个水杯分别是多少元?
(2)甲、乙两家商场同时出售同样的暖瓶和水杯,为了迎接新年,两家商场都在搞促销活动,甲商场规定: 这两种商品都打九折;乙商场规定:买一个暖瓶赠送一个水杯。若某单位想要买4个暖瓶和15个水杯,请问选择哪家商场购买更合算,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2 ![]() ,则线段CE的长为( )
,则线段CE的长为( ) 
A.![]()
B.8
C.2 ![]()
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形纸片ABCD中,AB=6,AD=10,点P是边BC上的动点,现将纸片折叠,使点A与点P重合,折痕与矩形边的交点分别为E、F,要使折痕始终与边AB、AD有交点,则BP的取值范围是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 |
B.平方差公式 |
C.两数和的完全平方公式 |
D.两数差的完全平方公式 |
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com