
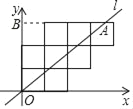
【题目】如图,将八个边长为1的小正方形摆放在平面直角坐标系中,若过原点的直线l将图形分成面积相等的两部分,则将直线l向右平移3个单位长度后所得直线l′的函数解析式为_____.
【答案】![]()
【解析】
设直线l和八个正方形的最上面交点为A,过点A作AB⊥y轴于点B,过点A作AC⊥x轴于点C,易知OB=3,利用三角形的面积公式和已知条件求出A的坐标,再利用待定系数法可求出该直线l的解析式,再根据平移规律即可得到直线l′的函数解析式.
解:设直线l和八个正方形的最上面交点为A,过A作AB⊥OB于B,过A作AC⊥OC于C,
∵正方形的边长为1,
∴OB=3,
∵经过原点的一条直线l将这八个正方形分成面积相等的两部分,
∴两边分别是4,
∴三角形ABO面积是5,
∴![]()
∴AB![]() ,
,
∴OC![]() ,
,
由此可知直线l经过![]()
设直线l为y=kx,
则![]()
![]()
∴直线l解析式为![]()
∴直线l向右平移3个单位长度后所得直线l′的函数解析式为![]()
故答案为:![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.
(1)假设每台冰箱降价x元,商场每天销售这种冰箱的利润是y元,请写出y与x之间的函数表达式;(不要求写自变量的取值范围)
(2)商场要想在这种冰箱销售中每天盈利4800元,同时又要使百姓得到实惠,每台冰箱应降价多少元?
(3)每台冰箱降价多少元时,商场每天销售这种冰箱的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
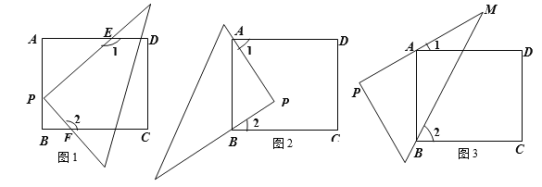
【题目】操作:将一个含30°角的直角三角形放在一长方形纸片上,
(1)如图1所示,直角顶点P在长方形的边AB上,直角边交长方形的两边AD、BC于点E、F,如果图中的∠1=140°,那么∠2= 度.
(2)如图2所示,直角顶点P在长方形内,且长方形的顶点A、B在∠P的直角边上,那么图中的∠1与∠2会有怎样的关系?为什么?
(3)如果将30°角如图3摆放,使得长方形的顶点A、B在30°角的两边上,此时,你认为图中的∠1与∠2会有怎样的关系?请直接写出你的结论: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,DE//BC,∠ADE=∠EFC,将说明∠1=∠2成立的理由填写完。
解:![]() DE//BC ( )
DE//BC ( )
![]() ∠ADE=_________ ( )
∠ADE=_________ ( )
![]() ∠ADE=∠EFC ( )
∠ADE=∠EFC ( )
![]() _____________=_____________ ( )
_____________=_____________ ( )
![]() DB//EF( )
DB//EF( )
![]() ∠1= ∠2 ( )
∠1= ∠2 ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料阅读:对于一个圆和一个正方形给出如下定义:若圆上存在到此正方形四条边距离都相等的点,则称这个圆是该正方形的“等距圆”.
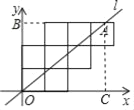
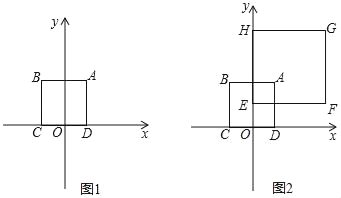
如图1,在平面直角坐标系xOy中,正方形ABCD的顶点A的坐标为(2,4),顶点C、D在x轴上,且点C在点D的左侧.
(1)当r=2![]() 时,在P1(2,0),P2(﹣4,2),P3(2
时,在P1(2,0),P2(﹣4,2),P3(2![]() ,2),P4(2﹣2
,2),P4(2﹣2![]() ,0)中可以成为正方形ABCD的“等距圆”的圆心的是 ;
,0)中可以成为正方形ABCD的“等距圆”的圆心的是 ;
(2)若点P坐标为(﹣2,﹣1),则当⊙P的半径r= 时,⊙P是正方形ABCD的“等距圆”.试判断此时⊙P与直线BD的位置关系?并说明理由.
(3)如图2,在正方形ABCD所在平面直角坐标系xOy中,正方形EFGH的顶点F的坐标为(8,2),顶点E、H在y轴上,且点H在点E的上方.若⊙P同时为上述两个正方形的“等距圆”,且与BC所在直线相切,求⊙P的圆心P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度y(m)与挖掘时间x(h)之间的关系如图所示.根据图象所提供的信息有:①甲队挖掘30m时,用了3h;②挖掘6h时甲队比乙队多挖了10m;③乙队的挖掘速度总是小于甲队;④开挖后甲、乙两队所挖河渠长度相等时,x=4.其中一定正确的有( )
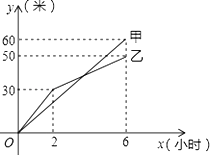
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
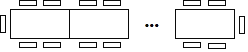
【题目】一种长方形餐桌的四周可坐6人用餐,现把若干张这样的餐桌按如图所示的方式进行拼接.
(1)若把4张这样的餐桌拼接起来,四周可坐 人;
(2)若把n张这样的餐桌拼接起来,四周可坐 人;
(3)若把9张这样的餐桌拼接起来,四周可坐 人;
(4)若用餐的人数有50人,则这样的餐桌需要多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解社区居民最喜欢的支付方式,某兴趣小组对龙湖社区内20~60岁年龄段的部分居民展开了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图.请根据图中信息解答下列问题:
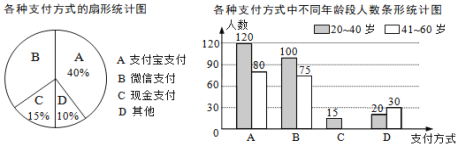
(1)求参与问卷调查的总人数.
(2)补全条形统计图.
(3)该社区中20~60岁的居民约4000人,估算这些人中最喜欢微信支付方式的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com