
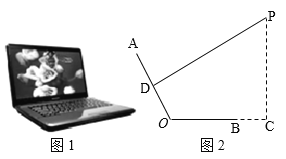
����Ŀ����ͼ1��һ̨������ˮƽ�����ϵıʼDZ����ԣ��������������ͼ2��ʾ�ļ���ͼ��.����ʾ��AO�����BO����Ϊ24cm����PΪ�۾�����λ�ã�DΪAO���е㣬����PD����PD��AO����ʱ��PΪ����ӽǣ�����C��OB���ӳ����ϣ�PC��BC��BC��12cm.
��1����PA��45cmʱ����PC�ij���
��2������AOC��115��ʱ���߶�PC�ij��ȣ�1�����߶�PC�ij��������Ǽ�С����ͨ������˵�����������ȷ��0.1cm��sin65���0.91��cos65���0.42��tan65���2.14��sin25���0.42��cos25���0.91��tan25���0.47��.
���𰸡���1��27![]() ��2������
��2������
��������
��1����PA��45cmʱ������PO�����ù��ɶ������PC��
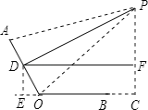
��2������AOC��115��ʱ������D��DE��OC��BO���ӳ�����E������D��DF��PC������ΪF������������Ǻ����ֱ����FC��PF���ɵõ���.
�⣺��1����PA��45cmʱ������PO��
��DΪAO���е㣬��PD��AO��
��PO��45cm.
��BO��24cm��BC��12cm����C��90�㣬
��OC��OB+BC��36cm��PC��![]() ��27cm��
��27cm��
��2������AOC��115��ʱ������D��DE��OC��BO���ӳ�����E������D��DF��PC������ΪF��
���ı���DECF�Ǿ��Σ�
��Rt��DOE��
�ߡ�AOE��65�㣬DO��![]() AO��12��
AO��12��
��DE��DOsin65�㣽12��0.91��10.92��EO��DO cos65�㣽12��0.42=5.04��
��FC��DE��10.92��DF��EC��EO+BO+BC��5.04+24+12��41.04��
��Rt��PDF��
�ߡ�PDF��25�㣬
��PF��DFtan25�㣽41.04��0.47��19.29��
��PC��PF+FC��19.29+10.92��30.2��27.
���߶�PC����������.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
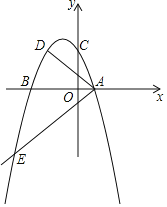
����Ŀ����ͼ�����κ���y��a��x2+2mx��3m2��������a��m�dz���a��0��m��0����ͼ����x��ֱ���A��B����Aλ�ڵ�B���Ҳࣩ����y�ύ�ڵ�C��0��3������D�ڶ��κ�����ͼ���ϣ�CD��AB������AD������A������AE�����κ�����ͼ���ڵ�E��ABƽ�֡�DAE��
��1����a��m�Ĺ�ϵʽ��
��2����֤��![]() Ϊ��ֵ��
Ϊ��ֵ��
��3����ö��κ�����ͼ��Ķ���ΪF��̽������x������������Ƿ���ڵ�G������GF�����߶�GF��AD��AE�ij���Ϊ���߳�����������ֱ�������Σ�������ڣ�ֻҪ�ҳ�һ������Ҫ��ĵ�G���ɣ����ú�m�Ĵ���ʽ��ʾ�õ�ĺ����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������y=![]() (x��0)����A(3��4)��ֱ��AC��x�ύ�ڵ�C(6��0)������C��x��Ĵ���BC������������ͼ���ڵ�B��
(x��0)����A(3��4)��ֱ��AC��x�ύ�ڵ�C(6��0)������C��x��Ĵ���BC������������ͼ���ڵ�B��
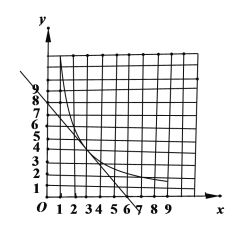
��1����գ������������Ľ���ʽΪ____________________��ֱ��AC�Ľ���ʽΪ____________________��B���������________��
��2����ƽ�����е�D��ʹ����A��B��C��D�ĵ�Ϊ���ı���Ϊƽ���ı��Σ�
����ͼ����ֱ�ߺ�2BǦ�ʻ������з���������ƽ���ı��Σ�
�ڸ��������Σ���ֱ��д���������������е�D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
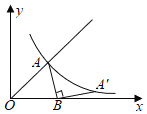
����Ŀ����ͼ������y��x��x��0����ͼ���뷴��������y��![]() ��ͼ���ڵ�A������A�Ƶ�B��
��ͼ���ڵ�A������A�Ƶ�B��![]() ��0��˳ʱ����ת90��õ��ĵ�A'����y��
��0��˳ʱ����ת90��õ��ĵ�A'����y��![]() ��ͼ���ϣ����A������Ϊ_____��
��ͼ���ϣ����A������Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������߱���ʽC��![]() �� ��֪��A(0��2)����P����������һ�㣬��Rt��AOP��һ���������ֵΪ
�� ��֪��A(0��2)����P����������һ�㣬��Rt��AOP��һ���������ֵΪ![]() �����P������_________________��
�����P������_________________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������κ���y=ax2+bx+c��a��0��ͼ��ĶԳ���Ϊx=1����y�ύ�ڵ�C����x�ύ�ڵ�A����B����1��0������
�ٶ��κ��������ֵΪa+b+c��
��a��b+c��0��
��b2��4ac��0��
�ܵ�y��0ʱ����1��x��3��������ȷ�ĸ����ǣ�������

A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
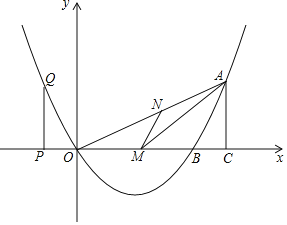
����Ŀ����ͼ����֪���κ�����ͼ�����O��0��0����A��8��4������x�ύ����һ��B���ҶԳ�����ֱ��x��3��
��1����ö��κ����Ľ���ʽ��
��2����M��OB�ϵ�һ�㣬��MN��AB��OA��N������ANM������ʱ����M�����ꣻ
��3��P��x���ϵĵ㣬��P��PQ��x���������߽���Q����A��AC��x����C������O��P��QΪ���������������O��A��CΪ���������������ʱ����P������꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������С����Ƶ������߶�ABΪһ���Խ�����һ���������ij߹���ͼ���̣�
��֪���߶�AB��
����������ACBD��
![]()
��������ͼ��
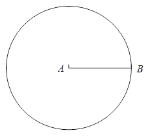
���Ե�AΪԲ�ģ���AB��Ϊ�뾶����A��
���Ե� BΪԲ�ģ���AB��Ϊ�뾶����B��
����A ��C��D���㣻
������AC��BC��BD��AD��
�����ı���ACBD���������������Σ�
����С����Ƶij߹���ͼ���̣�
��1��ʹ��ֱ�ߺ�Բ�棬��ȫͼ�Σ�������ͼ�ۼ�����
��2����������֤����
֤��������B��C��D����A�ϣ�
��AB=AC=AD( )�������������ݣ���
ͬ�� ����A��C��D����B�ϣ�
��AB=BC=BD��
�� = = = ��
���ı���ACBD�����Σ� ( )�������������ݣ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
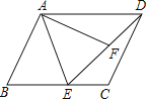
����Ŀ����ƽ���ı���ABCD�У�E��BC����һ�㣬F��DE��һ�㣬����B=��AFE��AB=AF��
��֤����1����ADF�ա�DEC����2��BE=EF��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com