
【题目】已知:线段 ![]() ,
, ![]() ,
, ![]() . 求作:矩形
. 求作:矩形 ![]() .
.
以下是甲、乙两同学的作业:
甲:① 以点 ![]() 为圆心,
为圆心, ![]() 长为半径作弧;
长为半径作弧;
② 以点 ![]() 为圆心,
为圆心, ![]() 长为半径作弧;
长为半径作弧;
③ 两弧在 ![]() 上方交于点
上方交于点 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
四边形 ![]() 即为所求矩形.(如图)
即为所求矩形.(如图)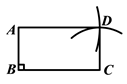
乙:① 连接 ![]() ,作线段
,作线段 ![]() 的垂直平分线,交
的垂直平分线,交 ![]() 于点
于点 ![]() ;
;
② 连接 ![]() 并延长,在延长线上取一点
并延长,在延长线上取一点 ![]() ,使
,使 ![]() ,连接
,连接 ![]() ,
, ![]() .
.
四边形 ![]() 即为所求矩形.(如图)
即为所求矩形.(如图)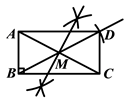
老师说甲、乙同学的作图都正确.
则甲的作图依据是:;
乙的作图依据是:.
【答案】两组对边分别相等的四边形是平行四边形;有一个角是直角的平行四边形是矩形;对角线互相平分的四边形是平行四边形;有一个角是直角的平行四边形是矩形.
【解析】解:由甲的作图方法可知AB=CD,BC=AD,根据两组对边分别相等的四边形是平行四边形即可判定四边形ABCD为平行四边形,又因∠ABC=90°,根据有一个角是直角的平行四边形是矩形 即可判定平行四边形ABCD为矩形;由乙的作图方法可知AM=BM,BM=DM,根据对角线互相平分的四边形是平行四边形即可判定四边形ABCD为平行四边形,又因∠ABC=90°,根据有一个角是直角的平行四边形是矩形 即可判定平行四边形ABCD为矩形.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形,以及对矩形的判定方法的理解,了解有一个角是直角的平行四边形叫做矩形;有三个角是直角的四边形是矩形;两条对角线相等的平行四边形是矩形.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F. 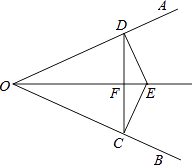
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60°,请你探究OE,EF之间有什么数量关系?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知C为线段AB的中点,D为线段AC的中点.
(1)画出相应的图形,求出图中线段的条数并写出相应的线段;
(2)若图中所有线段的长度和为26,求线段AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为直线AB上一点,∠AOC=58°,OD平分∠AOC,∠DOE=90°.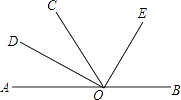
(1)求出∠BOD的度数;
(2)请通过计算说明:OE是否平分∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
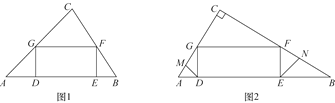
【题目】在面积为24的△ABC中,矩形DEFG的边DE在AB上运动,点F,G分别在边BC,AC上.
(1)若AB=8,DE=2EF,求GF的长;
(2)若![]() ,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
,如图2,线段DM,EN分别为△ADG和△BEF的角平分线,求证:MG=NF;
(3)求出矩形DEFG的面积的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抚州市正在争创省文明城市,为了美化城市,改善人们的居住环境,我市深入开展绿化彩化美化工程,通过植草、种树、修建公园及树阵式停车位等多项措施,使城区绿地面积不断增加.请根据图中所提供的信息,回答下列问题: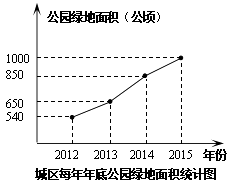
(1)2014年底的公园绿地面积为公顷,比2012年底增加了公顷;
(2)在2013年,2014年,2015年这三年中,绿地面积增加最多的是年;
(3)为满足城市发展的需要,计划到2017年底使城区公园绿地总面积达到1200公顷,试求2017年底公园绿地面积对2015年底的增长率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com