
【题目】如图,已知等腰梯形ABCD中,AD∥BC,AD=1,BC=3,AB=CD=2,点E在BC边上,AE与BD交于点F,∠BAE=∠DBC,
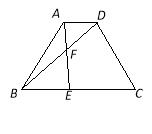
(1)求证:△ABE∽△BCD;
(2)求tan∠DBC的值;
(3)求线段BF的长.
【答案】(1)证明见解析(2)![]() (3)
(3)![]()
【解析】
试题分析:(1)根据条件∠BAE=∠DBC,再证明∠ABE=∠C,可得出结论;(2)分别过点A、D向BC边作垂线段,垂足分别为点G、H,证明△ABG≌△DCH 得出BG=HC,然后求出BH=2,利用勾股定理求出HD,然后利用正切的定义计算即可;(3)根据△ABE∽△BCD求出BE=![]() ,利用勾股定理求出BD的长,再根据
,利用勾股定理求出BD的长,再根据![]() =
=![]() ,求出BF的长.
,求出BF的长.
试题解析:(1)∵等腰梯形ABCD中,AD∥BC,∴∠ABE=∠C
又∵∠BAE=∠DBC ∴△ABE∽△BCD
(2)分别过点A、D向BC边作垂线段,垂足分别为点G、H
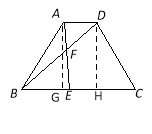
∵AD∥BC ∴AG=DH, 矩形AGHD中AG=DH,
又∵AB=CD∴△ABG≌△DCH ∴BG=HC
∵AD=1,BC=3 ,GH =1∴HC=(3-1)÷2=1, BH=2
∴在Rt△HDC中, HD=![]() =
=![]()
∴在Rt△BHD中, tan∠DBC=![]() =
=![]()
(3)∵△ABE∽△BCD ∴![]()
又∵BC=3,AB=CD=2,∴BE=![]()
∵AD∥BC , AD=1,![]() =
=![]()
又∵BD=![]() =
=![]() , ∴BF =
, ∴BF =![]()


科目:初中数学 来源: 题型:
【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要调查汇川区某所初中学校学生的平均体重,选取调查对象最合适的是( )
A. 选该校100名男生; B. 选该校100名女生;
C. 选该校七年级的两个班的学生; D. 在各年级随机选取100名学生。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断错误的是( )
A.两组对边分别相等的四边形是平行四边形
B.四个内角都相等的四边形是矩形
C.四条边都相等的四边形是菱形
D.两条对角线垂直且平分的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,探讨角平分线的作法时,李老师用直尺和圆规作角平分线,方法如下:


小颖的身边只有刻度尺,经过尝试,她发现利用刻度尺也可以作角平分线.
根据以上情境,解决下列问题:
①李老师用尺规作角平分线时,用到的三角形全等的判定方法是_________.
②小聪的作法正确吗?请说明理由.
③请你帮小颖设计用刻度尺作角平分线的方法.(要求:作出图形,写出作图步骤,不予证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某人在C处看到远处有一凉亭B,在凉亭B正东方向有一棵大树A,这时此人在C处测得B在北偏西45°方向上,测得A在北偏东35°方向上.又测得A、C之间的距离为100米,求A、B之间的距离.(精确到1米).(参考数据:sin35°≈0.574,cos35°≈0.819,tan35°≈0.700)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com