
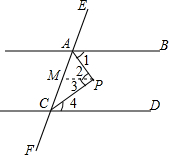
 已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.
已知:如图,AB∥CD,AP平分∠BAC,CP平分∠ACD,求∠APC的度数.分析 直接利用平行线的性质与判定以及平行公理分别分析得出答案.
解答 解:过P点作PM∥AB交AC于点M.
∵AB∥CD,( 已知)
∴∠BAC+∠ACD=180°. (两直线平行,同旁内角互补 )
∵PM∥AB,
∴∠1=∠2,(两直线平行,内错角相等)
且PM∥DC.(平行于同一直线的两直线也互相平行)
∴∠3=∠4. (两直线平行,内错角相等)
∵AP平分∠BAC,CP平分∠ACD,(已知)
∴∠1=$\frac{1}{2}$∠BAC,∠4=$\frac{1}{2}$ACD.
∴∠1+∠4=$\frac{1}{2}$∠BAC+$\frac{1}{2}$∠ACD=90°.
∴∠APC=∠2+∠3=∠1+∠4=90°.
总结:两直线平行时,同旁内角的角平分线互相垂直.
故答案为:已知;两直线平行,同旁内角互补;2;两直线平行,内错角相等,DC;4;两直线平行,内错角相等;已知;互相垂直.
点评 此题主要考查了平行线的性质以及平行公理等知识,正确利用平行线的性质分析是解题关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:解答题
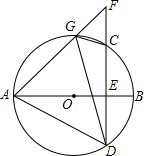 如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线交于点F,连接AD,GD,CG.
如图,AB是⊙O的直径,弦CD⊥AB于点E,G是弧AC上任意一点,延长AG,与DC的延长线交于点F,连接AD,GD,CG.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
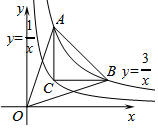 如图,点C在反比例函数y=$\frac{1}{x}$的图象上,CA∥y轴,交反比例函数y=$\frac{3}{x}$的图象于点A,CB∥x轴,交反比例函数y=$\frac{3}{x}$的图象于点B,连结AB、OA和OB,已知CA=2,则△ABO的面积为4.
如图,点C在反比例函数y=$\frac{1}{x}$的图象上,CA∥y轴,交反比例函数y=$\frac{3}{x}$的图象于点A,CB∥x轴,交反比例函数y=$\frac{3}{x}$的图象于点B,连结AB、OA和OB,已知CA=2,则△ABO的面积为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
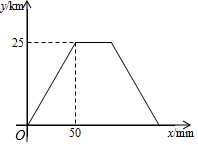 甲、乙两人骑车分别从A、B两地同时出发,沿同一路线匀速骑行,两人先相向而行,甲到达B地后停留20min再以原速返回A地,当两人到达A地后停止骑行.设甲出发xmin后距离A地的路程为ykm.图中的折线表示甲在整个骑行过程中y与x的函数关系.
甲、乙两人骑车分别从A、B两地同时出发,沿同一路线匀速骑行,两人先相向而行,甲到达B地后停留20min再以原速返回A地,当两人到达A地后停止骑行.设甲出发xmin后距离A地的路程为ykm.图中的折线表示甲在整个骑行过程中y与x的函数关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
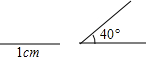 已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°(请在图中标出已知角的度数和已知边的长度,用直尺和圆规作图时,不写作法,保留作图痕迹).
已知一个三角形的两条边长分别是1cm和2cm,一个内角为40°(请在图中标出已知角的度数和已知边的长度,用直尺和圆规作图时,不写作法,保留作图痕迹).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com