
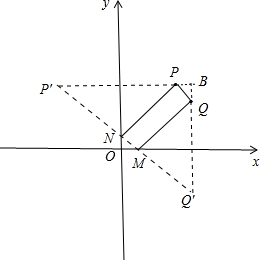
 解:(1)作点Q关于x轴的对称点Q′,作点P关于y轴的对称点P′,
解:(1)作点Q关于x轴的对称点Q′,作点P关于y轴的对称点P′,
|
|
| 72+72 |
| 2 |
| (4-3)2+(3-4)2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
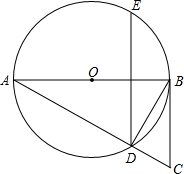 如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连接BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )
如图,在△ABC中,∠BAC=28°,以AB为直径的⊙O交AC于点D,DE∥CB,连接BD,若添加一个条件,使BC是⊙O的切线,则下列四个条件中不符合的是( )| A、DE⊥AB |
| B、∠EDB=28° |
| C、∠ADE=∠ABD |
| D、OB=BC |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )
如图为手的示意图,从大拇指开始,按食指,中指,无名指,小指,再回到大拇指的顺序,依次数正整数1,2,3,4,5当数到2015时,对应的手指( )| A、食指 | B、中指 | C、无名指 | D、小指 |
查看答案和解析>>
科目:初中数学 来源: 题型:
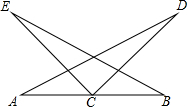 如图,有下列六个论断:①AC=CB,②∠A=∠B,③∠ACE=∠BCD,④CE=CD⑤∠E=∠D,⑥BE=AD.请以其中三个论断作为条件,编拟一个由三个条件能推出一个结论成立的真命题,并证明.
如图,有下列六个论断:①AC=CB,②∠A=∠B,③∠ACE=∠BCD,④CE=CD⑤∠E=∠D,⑥BE=AD.请以其中三个论断作为条件,编拟一个由三个条件能推出一个结论成立的真命题,并证明.查看答案和解析>>
科目:初中数学 来源: 题型:
| A、-2017 | B、2011 |
| C、-2013 | D、2017 |
查看答案和解析>>
科目:初中数学 来源: 题型:
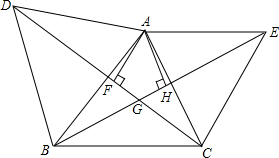 如图,已知△ABD、△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H.
如图,已知△ABD、△AEC都是等边三角形,AF⊥CD于F,AH⊥BE于H.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、①②③ | B、①③④ |
| C、③④ | D、①②③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com