
【题目】(1)如图1,在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为D,E.求证:DE=BD+CE;

(2)如图2,将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?若成立,请你给出证明;若不成立,请说明理由;
(3)如图3,在(2)的条件下,若a=120°,且△ACF为等边三角形,试判断△DEF的形状,并说明理由.
【答案】(1)见解析;(2)见解析;(3)△DEF为等边三角形。
【解析】
(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)利用∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°-α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案;
(3)证△BDF≌△AEF,得出DF=EF,∠BFD=∠AFE,而得出∠DFE=60°,即可推出△DEF为等边三角形.
证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
∵ ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中,
∵ ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
(3)△DEF为等边三角形,理由如下:
由(2)知△ADB≌△CEA,BD=AE,∠DBA=∠CAE,
∵△ACF为等边三角形,
∴∠CAF=60°,AF=AC,
又∵AB=AC,
∴AB=AF,
∵∠BAC=120°,
∴∠BAF=60°,
∴△ABF是等边三角形,
∴∠ABF=60°,BF=AF,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠EAF,
∵BF=AF,
∴△BDF≌△AEF(AAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形.


科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠A=90°,BC=10cm,点P、点Q同时从点B出发,点P以2cm/s的速度沿B→A→C运动,终点为C,点Q以1cm/s的速度沿B→C运动,当点P到达终点时两个点同时停止运动,设点P,Q出发t秒时,△BPQ的面积为ycm2 , 已知y与t的函数关系的图象如图2(曲线OM和MN均为抛物线的一部分),给出以下结论:①AC=6cm;②曲线MN的解析式为y=﹣ ![]() t2+
t2+ ![]() t(4≤t≤7);③线段PQ的长度的最大值为
t(4≤t≤7);③线段PQ的长度的最大值为 ![]() ;④若△PQC与△ABC相似,则t=
;④若△PQC与△ABC相似,则t= ![]() 秒.其中正确的是( )
秒.其中正确的是( )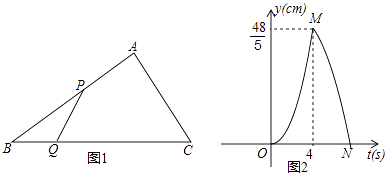
A.①②④
B.②③④
C.①③④
D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市开展一项自行车旅游活动,线路需经A,B,C,D四地,如图,其中A,B,C三地在同一直线上,D地在A地北偏东30°方向,在C地北偏西45°方向,C地在A地北偏东75°方向.且BC=CD=20km,问沿上述线路从A地到D地的路程大约是多少?(最后结果保留整数,参考数据:sin15°≈0.25,cos15°≈0.97,tan15°≈0.27, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】看图填空,并在括号内说明理由: 如图,已知∠BAP与∠APD互补,∠1=∠2,说明∠E=∠F.
证明:∵∠BAP与∠APD互补(_________), ∴AB∥CD(____________),
∴∠BAP=∠APC(__________).
又∵∠1=∠2(__________),
∴∠BAP﹣∠1=∠APC﹣∠2(_________),即∠3=∠4,
∴AE∥PF,(___________),
∴∠E=∠F(__________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=90°,OM平分∠AOB,将直角三角板的顶点P在射线OM上移动,两直角边分别与OA、OB相交于点C、D,问PC与PD相等吗?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将数轴按如图所示从某一点开始折出一个等边三角形ABC,设点A表示的数为x﹣3,点B表示的数为2x+1,点C表示的数为﹣4,若将△ABC向右滚动,则x的值等于_____,数字2012对应的点将与△ABC的顶点_____重合.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着市民环保意识的增强,节庆期间烟花爆竹销售量逐年下降.某市2012年销售烟花爆竹20万箱,到2014年烟花爆竹销售量为9.8万箱.求该市2012年到2014年烟花爆竹年销售量的平均下降率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com