
【题目】下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
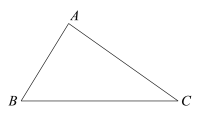
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴ = ( ) (填推理的依据) .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,将纸片展平,再次折叠纸片,使点A落在EF上的点N处,并使折痕经过点B,得到折痕BM,再展平纸片,连接MN,BN.下列结论一定正确的是( )
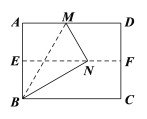
A.![]() B.
B.![]()
C.BM与EN互相平分D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B的坐标分别为(1,4)和(4,4),抛物线y=a(x+m)2+n的顶点在线段AB上,与x轴交于C,D两点(C在D的左侧),点C的横坐标最小值为﹣3,则点D的横坐标的最大值为_____.
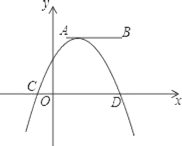
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“在已知三角形的一边上取一点,使得这点到这个三角形的另外两边的距离相等”的尺规作图过程:
已知:△ABC.
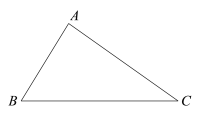
求作:点D,使得点D在BC边上,且到AB,AC边的距离相等.
作法:如图,
作∠BAC的平分线,交BC于点D.则点D即为所求.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形 (保留作图痕迹);
(2)完成下面的证明.
证明:作DE⊥AB于点E,作DF⊥AC于点F,
∵AD平分∠BAC,
∴ = ( ) (填推理的依据) .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,E是CD边上一点(CE>DE),AE,BD交于点F.
(1)如图1,过点F作GH⊥AE,分别交边AD,BC于点G,H.
求证:∠EAB=∠GHC;
(2)AE的垂直平分线分别与AD,AE,BD交于点P,M,N,连接CN.
①依题意补全图形;
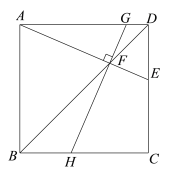
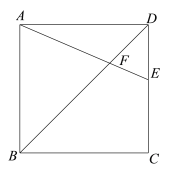
图1 备用图
②用等式表示线段AE与CN之间的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象G与直线
)的图象G与直线![]() 交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
交于点A(4,1),点B(1,n)(n≥4,n为整数)在直线l上.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 与直线l围成的区域(不含边界)为W.
与直线l围成的区域(不含边界)为W.
①当n=5时,求![]() 的值,并写出区域W内的整点个数;
的值,并写出区域W内的整点个数;
②若区域W内恰有5个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)“六·一”儿童节前,某玩具商店根据市场调查,用2500元购进一批儿童玩
具,上市后很快脱销,接着又用4500元购进第二批这种玩具,所购数量是第一批数量的1.5
倍,但每套进价多了10元.
(1)求第一批玩具每套的进价是多少元?
(2)如果这两批玩具每套售价相同,且全部售完后总利润不低于25%,那么每套售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一部记录片播放了关于地震的资料及一个有关地震预测的讨论,一位专家指出:“在未来20年,A城市发生地震的机会是三分之二”
对这位专家的陈述下面有四个推断:
①![]() ×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
×20≈13.3,所以今后的13年至14年间,A城市会发生一次地震;
②![]() 大于50%,所以未来20年,A城市一定发生地震;
大于50%,所以未来20年,A城市一定发生地震;
③在未来20年,A城市发生地震的可能性大于不发生地震的可能性;
④不能确定在未来20年,A城市是否会发生地震;
其中合理的是( )
A. ①③ B. ②③ C. ②④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某中学学生课余生活情况,对喜爱看课外书、体育活动、看电视、社会实践四个方面的人数进行调查统计.现从该校随机抽取![]() 名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
名学生作为样本,采用问卷调查的方法收集数据(参与问卷调查的每名学生只能选择其中一项).并根据调查得到的数据绘制成了如图所示的两幅不完整的统计图.由图中提供的信息,解答下列问题:
(1)求n的值;
(2)若该校学生共有1200人,试估计该校喜爱看电视的学生人数;
(3)若调查到喜爱体育活动的4名学生中有3名男生和1名女生,现从这4名学生中任意抽取2名学生,求恰好抽到2名男生的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com