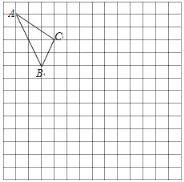
【题目】如图，在正方形网格中，每一个小正方形的边长为1．格点三角形ABC（顶点是网格线交点的三角形）的顶点A，C的坐标分别是（﹣4，6），（﹣1，4）．
（1）请在图中的网格平面内建立平面直角坐标系（直接在图中画出）；
（2）请画出△ABC关于x轴对称的△A1B1C1；
（3）写出点A1、C1的坐标．
科目：初中数学 来源： 题型：
【题目】一只口袋里放着
个红球、
个黑球和若干个白球，这三种球除颜色外没有任何区别，并搅匀．
取出红球的概率为
，白球有多少个？
取出黑球的概率是多少？
再在原来的袋中放进多少个红球，能使取出红球的概率达到
？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】我们新定义一种三角形：若一个三角形中存在两边的平方差等于第三边上高的平方，则称这个三角形为勾股高三角形，两边交点为勾股顶点．
●特例感知
①等腰直角三角形 勾股高三角形（请填写“是”或者“不是”）；
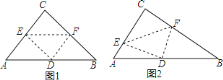
②如图1，已知△ABC为勾股高三角形，其中C为勾股顶点，CD是AB边上的高．若
，试求线段CD的长度．
●深入探究
如图2，已知△ABC为勾股高三角形，其中C为勾股顶点且CA＞CB，CD是AB边上的高．试探究线段AD与CB的数量关系，并给予证明；
●推广应用
如图3，等腰△ABC为勾股高三角形，其中
，CD为AB边上的高，过点D向BC边引平行线与AC边交于点E．若
，试求线段DE的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在
中，
，翻折
，使点
落在斜边
上某一点
处，折痕为
（点
、
分别在边
、
上）
当
时，若
与
相似（如图
），求
的长；
当点是的中点时（如图
），与相似吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1，点C在线段AB上，（点C不与A、B重合），分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE，连接AE、BD交于点P．
（观察猜想）
①AE与BD的数量关系是 ；
②∠APD的度数为 ．
（数学思考）
如图2，当点C在线段AB外时，（1）中的结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明；
（拓展应用）
如图3，点E为四边形ABCD内一点，且满足∠AED＝∠BEC＝90°，AE＝DE，BE＝CE，对角线AC、BD交于点P，AC＝10，则四边形ABCD的面积为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，点P在长方形OABC的边OA上，连接BP，过点P作BP的垂线，交射线OC于点Q，在点P从点A出发沿AO方向运动到点O的过程中，设AP=x，OQ=y，则下列说法正确的是（ ）
A.y随x的增大而增大B.y随x的增大而减小
C.随x的增大，y先增大后减小D.随x的增大，y先减小后增大
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
