
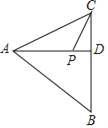
【题目】如图,在△ABC中,AD是高,BD=6,CD=4,tan∠BAD=![]() ,P是线段AD上一动点,一机器人从点A出发沿AD以
,P是线段AD上一动点,一机器人从点A出发沿AD以![]() 个单位/秒的速度走到P点,然后以1个单位/秒的速度沿PC走到C点,共用了t秒,则t的最小值为_____.
个单位/秒的速度走到P点,然后以1个单位/秒的速度沿PC走到C点,共用了t秒,则t的最小值为_____.
【答案】8
【解析】
作PH⊥AB于H,根据锐角三角函数求得AD=8,根据勾股定理求得AB=10,设机器从A运动到P点用x秒,则从P点运动到C用了(t﹣x)秒,当点C、P、H共线时,PC+PH的值最小,即t的值最小,可求得t的最小值.
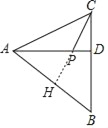
解:作PH⊥AB于H,如图,
∵AD是高,
∴∠ADB=∠ADC=90°,
∵tan∠BAD=![]() =
=![]() ,
,
∴AD=![]() ×6=8,
×6=8,
∴AB=![]() =10,
=10,
设机器从A运动到P点用x秒,则从P点运动到C用了(t﹣x)秒,
∴AP=![]() x,PC=t﹣x,
x,PC=t﹣x,
在Rt△ABD中,sin∠BAD=![]() =
=![]() =
=![]() ,
,
在Rt△APH中,sin∠PAH=![]() =
=![]() ,
,
∴PH=![]()
![]() x=x,
x=x,
∴PC+PH=x+t﹣x=t,
而点C、P、H共线时,PC+PH的值最小,即t的值最小,
此时CH⊥AB,
在Rt△ABD中,sinB=![]() =
=![]() =
=![]() ,
,
在Rt△BCH中,∴sin∠B=![]() =
=![]() ,
,
∴CH=![]() ×(4+6)=8,
×(4+6)=8,
即t的最小值为8.
故答案为8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明和小亮玩一个游戏:三张大小、质地都相同的卡片上分别标有数字2,3,4(背面完全相同),现将标有数字的一面朝下.小明从中任意抽取一张,记下数字后放回洗匀,然后小亮从中任意抽取一张,计算小明和小亮抽得的两个数字之和.若和为奇数,则小明胜;若和为偶数,则小亮胜.
(1)请你用画树状图或列表的方法,求出这两数和为6的概率.
(2)你认为这个游戏规则对双方公平吗?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有2名男生和2名女生获得音乐奖.
(1)从获得美术奖和音乐奖的7名学生中选取1名参加颁奖大会,求刚好是男生的概率;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016湖南省株洲市)某市对初二综合素质测评中的审美与艺术进行考核,规定如下:考核综合评价得分由测试成绩(满分100分)和平时成绩(满分100分)两部分组成,其中测试成绩占80%,平时成绩占20%,并且当综合评价得分大于或等于80分时,该生综合评价为A等.
(1)孔明同学的测试成绩和平时成绩两项得分之和为185分,而综合评价得分为91分,则孔明同学测试成绩和平时成绩各得多少分?
(2)某同学测试成绩为70分,他的综合评价得分有可能达到A等吗?为什么?
(3)如果一个同学综合评价要达到A等,他的测试成绩至少要多少分?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高3米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有27米的距离(B,F,C在一条直线上).

(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
(参考数据:sin22°≈![]() ,cos22°≈
,cos22°≈![]() ,tan22°≈
,tan22°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
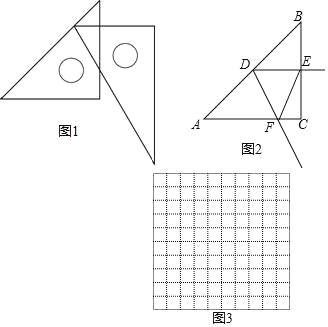
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图1摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=_____°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | ____ | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2015年2月27日,在中央全面深化改革领导小组第十次会议上,审议通过了《中国足球改革总体方案》,体制改革、联赛改革、校园足球等成为改革的亮点.在联赛方面,作为国内最高水平的联赛﹣﹣中国足球超级联赛今年已经进入第12个年头,中超联赛已经引起了世界的关注.图9是某一年截止倒数第二轮比赛各队的积分统计图.

(1)根据图,请计算该年有_____支中超球队参赛;
(2)补全图一中的条形统计图;
(3)根据足球比赛规则,胜一场得3分,平一场得1分,负一场得0分,最后得分最高者为冠军.倒数第二轮比赛后积分位于前4名的分别是A队49分,B队49分,C队48分,D队45分.在最后一轮的比赛中,他们分别和第4名以后的球队进行比赛,已知在已经结束的一场比赛中,A队和对手打平.请用列表或者画树状图的方法,计算C队夺得冠军的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出
(1)如图①,在△ABC中,∠A=120°,AB=AC=5,则△ABC的外接圆半径R的值为 .
问题探究
(2)如图②,⊙O的半径为13,弦AB=24,M是AB的中点,P是⊙O上一动点,求PM的最大值.
问题解决
(3)如图③所示,AB、AC、BC是某新区的三条规划路其中,AB=6km,AC=3km,∠BAC=60°,BC所对的圆心角为60°.新区管委会想在BC路边建物资总站点P,在AB、AC路边分别建物资分站点E、F.也就是,分别在![]() 、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).
、线段AB和AC上选取点P、E、F.由于总站工作人员每天要将物资在各物资站点间按P→E→F→P的路径进行运输,因此,要在各物资站点之间规划道路PE、EF和FP.为了快捷环保和节约成本要使得线段PE、EF、FP之和最短,试求PE+EF+FP的最小值(各物资站点与所在道路之间的距离、路宽均忽略不计).



图① 图② 图③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com