
 将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )
将一列整数1,2,3,-4,-5,-6,7,-8,-9,-10,…按如图所示排列.如第一个顶峰的数是-6,第二个峰顶的数是15,那么第2016个峰顶的数是( )| A. | 18150 | B. | -18150 | C. | 18141 | D. | -18141 |
分析 先观察发现从第一个峰顶到第二个峰顶之间一共有9个数,且不看符号,后面的数比前面的数大1,即是连续整数,所以后面的峰顶数比前面的峰顶数大9,得出第n个峰顶的数是:6+9(n-1)=9n-3,计算出第2016个峰顶的数,再考虑符号:第奇数峰顶的数为负数,第偶数峰顶的数为正数;从而得出结论.
解答 解:①先不考虑符号:
第一个峰顶的数是:6,
第二个峰顶的数是:15=6+9,
第三个峰顶的数是:15+9=6+9×2=24,
…
则第n个峰顶的数是:6+9(n-1)=9n-3,
∴第2016个峰顶的数是:6+9×2015=18141,
②看符号:第奇数峰顶的数为负数,第偶数峰顶的数为正数;
∴第2016个峰顶的数是:18141;
故选C.
点评 本题是数字类的规律题,此类题的解题思路为:认真观察同类数,即每一个峰顶的数的关系,可以从两方面考虑:①绝对值,即数字,②符号;发现规律并验证,从而得出结论.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
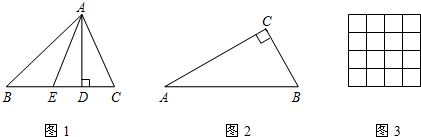
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
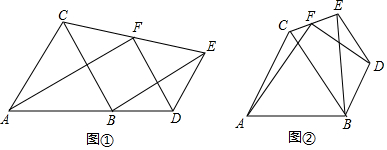 如图①,△ABC为等边三角形,D为AB延长线上一点,BD=DE.∠BDE=120°,连接EB、EC,F为EC的中点,连接FA、FD.
如图①,△ABC为等边三角形,D为AB延长线上一点,BD=DE.∠BDE=120°,连接EB、EC,F为EC的中点,连接FA、FD.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
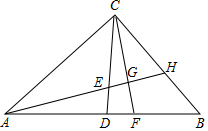 如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E,F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止.直线AE分别与CF、BC相于点G、H,则在点E、F移动的过程中,点G移动路线的长度为( )
如图,在△ABC中,∠ACB=90°,AC=BC,AB=4cm,CD是中线,点E,F同时从点D出发,以相同的速度分别沿DC、DB方向移动,当点E到达点C时,运动停止.直线AE分别与CF、BC相于点G、H,则在点E、F移动的过程中,点G移动路线的长度为( )| A. | 2 | B. | π | C. | $\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com