Question

13．在如图所示的直角坐标系中，点C坐标为（7，3）．回答下列问题：
（1）找到图中点C的位置；
（2）求出四边形OBCD的周长；
（3）求出四边形OBCD的面积．

Answer 1

分析 在坐标系中描出各点，可把四边形OBCD看成两个三角形和一个梯形，利用面积的和可求得四边形OBCD的面积．

解答 解：（1）点C的位置如图：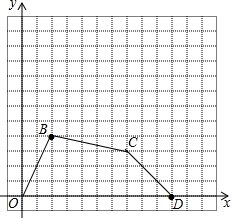

（2）四边形OBCD的周长=$\sqrt{{2}^{2}+{4}^{2}}+\sqrt{1+{5}^{2}}+\sqrt{{3}^{2}+{3}^{2}}+10$=$2\sqrt{5}+\sqrt{26}+3\sqrt{2}+10$；
四边形OBCD的面积=$\frac{1}{2}×2×3+\frac{1}{2}×3×3+\frac{1}{2}×（3+4）×5$=25．

点评 本题主要考查点的坐标与三角形的面积，求不规则图形的面积的方法就是“割”或“补”，即把不规则的图形转化成规则图形的和或差．