
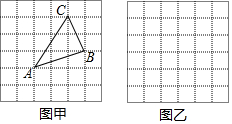
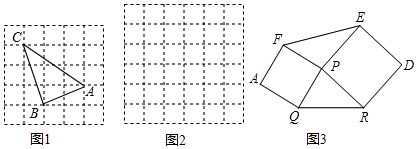
���� ��1�����ø�����ɵã�
��2�����ݹ��ɶ����������л�����Ӧ�ġ�ABC�����ݾ��ε������ʽ�������ε������ʽ������������
��3����ϣ�1������2���ô������ε����߷ֱ���ֱ�DZ߳�Ϊm��4n��ֱ�������ε�б�ߣ�ֱ�DZ߳�Ϊ3m��2n��ֱ�������ε�б�ߣ�ֱ�DZ߳�Ϊ2m��2n��ֱ�������ε�б�ߣ�ͬ����������Ϊһ�����ε������ȥ����ֱ�������ε������
��� �⣺��1����ABC�����=3��3-$\frac{1}{2}$��3��1-$\frac{1}{2}$��1��2-$\frac{1}{2}$��2��3=$\frac{7}{2}$��
�ʴ�Ϊ��$\frac{7}{2}$��
��2����ͼ2��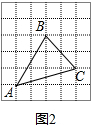
��ABC�����=3a��4a-$\frac{1}{2}$��3a��2a-$\frac{1}{2}$��a��4a-$\frac{1}{2}$��2a��2a=5a2��
��3�������ABC��ʾ��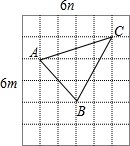
S��ABC=3m��4n-$\frac{1}{2}$��m��4n-$\frac{1}{2}$��3m��2n-$\frac{1}{2}$��2m��2n=5mn��
���� ���⿼����ǹ��ɶ�����Ӧ�ã��������κ�һ��ֱ���������У�����ֱ�DZ߳���ƽ��֮��һ������б�߳���ƽ���ǽ���Ĺؼ���


 �ʰ�Ӣ��ͬ����ϰ��ϵ�д�
�ʰ�Ӣ��ͬ����ϰ��ϵ�д� ѧϰʵ����ϵ�д�
ѧϰʵ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��1����֪x+y=4��x2+y2=9����xy��ֵ��
��1����֪x+y=4��x2+y2=9����xy��ֵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
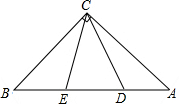 ��ͼ���ڵ���ֱ�ǡ�ABC�У�AC=BC����BCA=90�㣬D��EΪб��AB�ϵĵ㣬��DCE=45�㣬��AD=2��DE=5����BE�ij��ǣ�������
��ͼ���ڵ���ֱ�ǡ�ABC�У�AC=BC����BCA=90�㣬D��EΪб��AB�ϵĵ㣬��DCE=45�㣬��AD=2��DE=5����BE�ij��ǣ�������| A�� | 3 | B�� | $\frac{9}{2}$ | C�� | $\sqrt{19}$ | D�� | $\sqrt{21}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
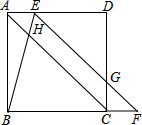 ��ͼ����������ABCD�У���E�ڱ�AD�ϣ���F�ڱ�BC���ӳ����ϣ�����EF���CD�ཻ�ڵ�G������BE��Խ���AC�ཻ�ڵ�H��AE=CF��BE=EG��
��ͼ����������ABCD�У���E�ڱ�AD�ϣ���F�ڱ�BC���ӳ����ϣ�����EF���CD�ཻ�ڵ�G������BE��Խ���AC�ཻ�ڵ�H��AE=CF��BE=EG���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
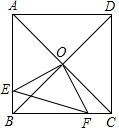 ��ͼ����������ABCD�У�O�ǶԽ���AC��BD�Ľ��㣮����O��OE��OF���ֱ�AB��BC�ڵ�E��F����AE=3��CF=1����EF=��������
��ͼ����������ABCD�У�O�ǶԽ���AC��BD�Ľ��㣮����O��OE��OF���ֱ�AB��BC�ڵ�E��F����AE=3��CF=1����EF=��������| A�� | 2 | B�� | $\sqrt{10}$ | C�� | 4 | D�� | 2$\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com