
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
 如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.
如图,在四边形ABCD中,M、N分别是对角线AC、BD的中点,又AD、BC的延长线交于P,求证:S△PMN=$\frac{1}{4}$S四边形ABCD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
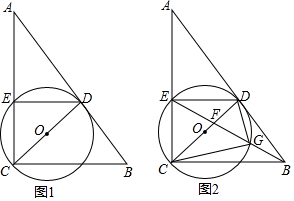
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
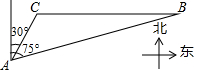 如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)
如图,BC是某公园人工湖中的两个人造观光小岛,为了测量两个小岛BC之间的距离,工作人员在距离小岛C 100米的地方选择了一个固定观测点A,并测得小岛C在观侧点A北偏东30°的方向上,与此同时,工作人员还测得小岛B在观测点A北偏东75°的方向上,请你利用工作人员测得的相关数据,计算观光小岛BC之间的距离.(结果精确到0.1米,参考数据:$\sqrt{3}$≈1.732,sin75°≈0.9659,cos75°≈0.2588,tan75°≈3.7321)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知点A(-2,-4),直线x=-2与x轴相交于点B,连接OA,抛物线y=-x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到点A时停止移动.
如图,在平面直角坐标系中,已知点A(-2,-4),直线x=-2与x轴相交于点B,连接OA,抛物线y=-x2从点O沿OA方向平移,与直线x=-2交于点P,顶点M到点A时停止移动.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
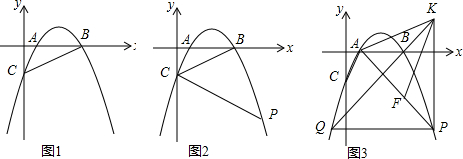
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com