
分析 (1)先算负整数指数幂,平方,零指数幂,再相减计算即可求解;
(2)有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,最后合并同类项即可求解;
(3)先根据完全平方公式和平方差公式计算,最后合并同类项即可求解;
(4)先变形为[(-2a+3)-b][(-2a+3)+b],再根据平方差公式和完全平方公式计算,最后合并同类项即可求解.
解答 解:(1)${3^0}-{2^{-3}}+{(-3)^2}-{(\frac{1}{4})^{-1}}$
=1-$\frac{1}{8}$+9-4
=5$\frac{7}{8}$
(2)(-2x2)3+x2•x4-(-3x3)2
=-8x6+x6-9x6
=-16x6;
(3)(x+2)2-(x+1)(x-1)
=x2+4x+4-x2+1
=4x+5;
(4)(-2a-b+3)(-2a+b+3)
=[(-2a+3)-b][(-2a+3)+b]
=(-2a+3)2-b2
=4a2-12a+9-b2.
点评 考查了整式的混合运算,“整体”思想在整式运算中较为常见,适时采用整体思想可使问题简单化,并且迅速地解决相关问题,此时应注意被看做整体的代数式通常要用括号括起来.


科目:初中数学 来源: 题型:选择题
| A. | 2016x2015 | B. | 2016x2016 | C. | 4032x2015 | D. | 4032x2016 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
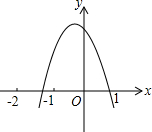 如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )
如图,二次函数y=ax2+bx+c(a≠0)的图象过点(-1,2)且与x轴交点的横坐标分别为x1,x2,其中-2<x1<-1,0<x2<1,下列结论:①4a-2b+c<0;②2a-b<0;③b2+8a>4ac;④abc>0,其中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
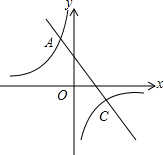 如图,点C是反比例函数y=$\frac{k}{x}$(k<0)图象上的一点,点C的坐标为(4,k+3).
如图,点C是反比例函数y=$\frac{k}{x}$(k<0)图象上的一点,点C的坐标为(4,k+3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
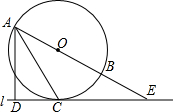 如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.
如图,AB为⊙O的直径,直线l与⊙O相切于点C,交AB的延长线于点E,过点A作AD⊥CE于点D,连接AC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com