
【题目】如图,在△ABC中,AC=BC,以BC边为直径作⊙O交AB边于点D,过点D作DE⊥AC于点E.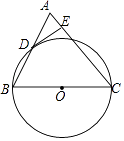
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径等于 ![]() ,cosB=
,cosB= ![]() ,求线段DE的长.
,求线段DE的长.
【答案】
(1)解:证明:连结OD.
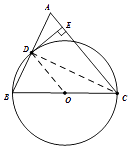
∵AC=BC,
∴∠A=∠B,
∵OB=OD,
∴∠B=∠ODB,
∴∠A=∠ODB,
∴OD∥AC,
∵DE⊥AC,
∴DE⊥OD,
∴DE是⊙O的切线,
(2)解:如图,连结CD.

∵⊙O的半径等于 ![]() ,
,
∴BC=3,∠CDB=90°,
在Rt△CDB中,
cosB= ![]() =
= ![]() ,
,
∴BD=1, ![]() ,
,
∵AC=BC=3,∠CDB=90°.
∴AD=BD=1,
解法一:在Rt△ADC中, ![]() ,
,
解法二:∵∠A=∠A,∠ADC=∠AED=90°,
∴△ACD∽△ADE.
∴ ![]() .
.
∴ ![]()
【解析】(1)根据等腰三角形的性质,等边对等角,得到角相等,得出平行线,得出DE是⊙O的切线;(2)根据在Rt△CDB中,由三角函数和勾股定理求出AC=BC、CD、AD=BD的值,由角相等得出△ACD∽△ADE,得到比例,求出DE的值.
【考点精析】通过灵活运用等腰三角形的性质和解直角三角形,掌握等腰三角形的两个底角相等(简称:等边对等角);解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.


科目:初中数学 来源: 题型:
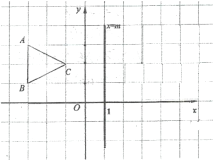
【题目】如图,在平面直角坐标系中,有△ABC和x=m直线.
(1)若A(-3,3),B (-3,1),C (-1,2),当m=1时,在图中作出△ABC关于直线x=m对称的图形,并直接写出![]() ,
,![]() ,
,![]() 的对应点
的对应点![]() ,
,![]() ,
,![]() 的坐标;
的坐标;
(2)若又有点![]() 和点
和点![]() 关于直线
关于直线![]() 对称,那么
对称,那么![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 之间有什么数量关系?(直接写出答案即可)
之间有什么数量关系?(直接写出答案即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一个正方形纸片OABC放置在平面直角坐标系中,其中A(1,0),C(0,1),P为AB边上一个动点,折叠该纸片,使O点与P点重合,折痕l与OP交于点M,与 对角线AC交于Q点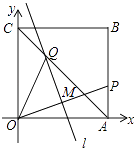
(Ⅰ)若点P的坐标为(1, ![]() ),求点M的坐标;
),求点M的坐标;
(Ⅱ)若点P的坐标为(1,t)
①求点M的坐标(用含t的式子表示)(直接写出答案)
②求点Q的坐标(用含t的式子表示)(直接写出答案)
(Ⅲ)当点P在边AB上移动时,∠QOP的度数是否发生变化?如果你认为不发生变化,写出它的角度的大小.并说明理由;如果你认为发生变化,也说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )
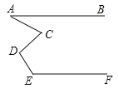
A. ∠A+∠C+∠D+∠E=360°B. ∠A-∠C+∠D+∠E=180°
C. ∠E-∠C+∠D-∠A=90°D. ∠A+∠D=∠C+∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了落实漳州市教育局关于全市中小学生每天阅读1小时的文件精神.某校对七年级(3)班全体学生一周到图书馆的次数做了调查统计,以下是调查过程中绘制的还不完整的两个统计图.请你根据统计图表中的信息,解答下列问题:
七年级(3)班学生到图书馆的次数统计表
到图书馆的 | 0次 | 1次 | 2次 | 3次 | 4次及 |
人数 | 5 | 10 | m | 8 | 12 |
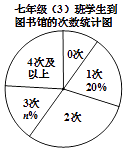
(1)求图表中m,n的值;
(2)该年级学生共有300人,估计这周到图书馆的次数为“4次及以上”的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,点E、F分别是AB、CD的中点,过点E作AB的垂线,过点F作CD的垂线,两垂线交于点G,连接AG、BG、CG、DG,且∠AGD=∠BGC.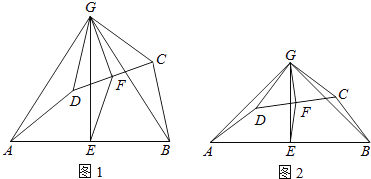
(1)求证:AD=BC;
(2)求证:△AGD∽△EGF;
(3)如图2,若AD、BC所在直线互相垂直,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC=AD,∠CAD=60°,分别连接BC、BD,作AE平分∠BAC交BD于点E,若BE=4,ED=8,则DF=_____.
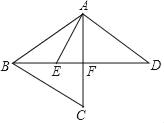
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四川雅安地震牵动全国人民的心,同学们都在积极进行捐款活动.某校九(2)班同学人人拿出自己的零花钱,踊跃募捐,学生捐款额有5元、10元、15元、20元四种情况.根据统计数据绘制了图①和图②两幅尚不完整的统计图.则该班同学平均捐款 ( )
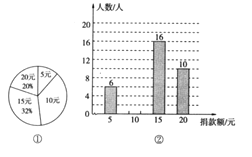
A. 12元 B. 12.5元 C. 13元 D. 13.5元
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com