
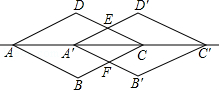
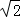 ������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���
������A��FCE�����������ABCD�����һ�룬��ƽ�Ƶľ���AA��ij���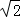 ��1����AC��A��C=
��1����AC��A��C=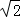 ��1����7�֣�
��1����7�֣�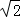 ��
��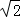 ��1����10�֣�
��1����10�֣�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ��
���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
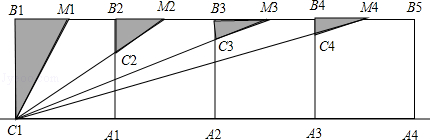
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
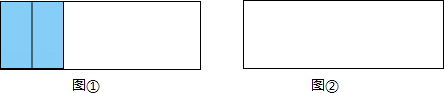
| A�����еľ��ζ����� |
| B����һ�������ȵ�ֱ������������ |
| C��������ͬ�Ķ����һ������ |
| D�����еĵ������������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
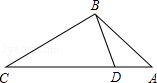
| A����ABD=��C | B����ADB=��ABC | C��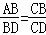 | D��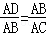 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
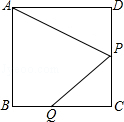
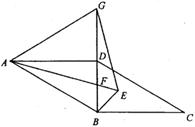
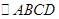 �У��Խ���
�У��Խ���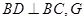 ΪBD�ӳ�����һ����
ΪBD�ӳ�����һ����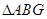 Ϊ�ȱ������Σ�
Ϊ�ȱ������Σ�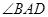 ��
��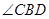 ��ƽ�����ཻ�ڵ�
��ƽ�����ཻ�ڵ�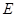 ������
������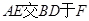 ������
������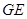 ��
��
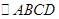 �����Ϊ
�����Ϊ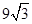 ����
����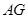 �ij���
�ij���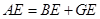 ��
���鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com