
 如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.
如图,自△ABC的外接圆弧BC上的任一点M,作MD⊥BC于D,P是AM上一点,作PE⊥AC,PF⊥AB,PG⊥BC,E,F,G分别在AC,AB,AD上.证明:E,F,G三点共线.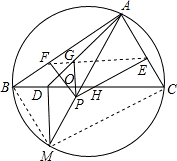
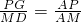 ,…①
,…① ,…②
,…②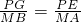 ,
,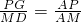 ,证△APE∽△BMD,
,证△APE∽△BMD, ,推出
,推出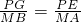 ,根据∠GPE=∠ACB=∠BMA,推出△PEG∽△MAB,求出∠PGE=∠ABM,∠PGF=∠ACM,由圆内接四边形性质得:∠PGE+∠PGF=180°即可.
,根据∠GPE=∠ACB=∠BMA,推出△PEG∽△MAB,求出∠PGE=∠ABM,∠PGF=∠ACM,由圆内接四边形性质得:∠PGE+∠PGF=180°即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com