
 如图,某渔船在A处观测到灯塔M在它的北偏东48°方向上,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在它的北偏东37°方向上.这艘渔船继续向正东航行多少海里,距离灯塔M最近?(参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin48°≈$\frac{7}{10}$,tan48°≈$\frac{11}{10}$,cos37°≈$\frac{4}{5}$,cos48°≈$\frac{7}{11}$)
如图,某渔船在A处观测到灯塔M在它的北偏东48°方向上,这艘渔船以每小时28海里的速度向正东方向航行,半小时后到达B处,在B处观测到灯塔M在它的北偏东37°方向上.这艘渔船继续向正东航行多少海里,距离灯塔M最近?(参考数据:sin37°≈$\frac{3}{5}$,tan37°≈$\frac{3}{4}$,sin48°≈$\frac{7}{10}$,tan48°≈$\frac{11}{10}$,cos37°≈$\frac{4}{5}$,cos48°≈$\frac{7}{11}$) 分析 过M作MC⊥AB,交AB延长线于点C,设BC=x,在Rt△AMC和Rt△BCM中,可用x分别表示出MC,可求得x的值,即可求得答案.
解答 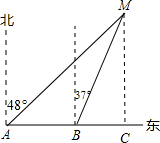 解:
解:
如图,过M作MC⊥AC,交AB延长线于点C,则当渔船航行到C点时,距离灯塔最近.
由题意可知∠AMC=48°,∠BMC=37°,AB=28×$\frac{1}{2}$=14海里,
设BC=x,则AC=14+x,
在RtRt△AMC中,MC=$\frac{AC}{tan∠AMC}$=$\frac{14+x}{\frac{11}{10}}$,
和Rt△BCM中,MC=$\frac{BC}{tan∠BMC}$=$\frac{x}{\frac{3}{4}}$,
∴$\frac{14+x}{\frac{11}{10}}$=$\frac{x}{\frac{3}{4}}$,解得x=30,
答:这艘渔船继续向正东航行30海里,距离灯塔最近.
点评 本题主要考查解三角形,熟练掌握三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
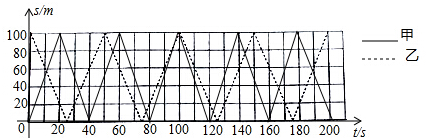
| 两人相遇次数(单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和(单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com