
【题目】如图,在正方形ABCD中,点E在边CD上(不与点C,D重合),连接AE,BD交于点F.
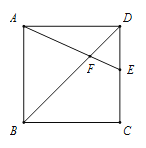
(1)若点E为CD中点,AB=2![]() ,求AF的长.
,求AF的长.
(2)若![]() ∠AFB=2,求
∠AFB=2,求![]() 的值.
的值.
(3)若点G在线段BF上,且GF=2BG,连接AG,CG,设![]() =x,四边形AGCE的面积为
=x,四边形AGCE的面积为![]() ,
,![]() ABG的面积为
ABG的面积为![]() ,求
,求![]() 的最大值.
的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)由![]() 可得DE的长,利用勾股定理可得AE的长,又易证
可得DE的长,利用勾股定理可得AE的长,又易证![]() ,由相似三角形的性质可得
,由相似三角形的性质可得![]() ,求解即可得;
,求解即可得;
(2)如图(见解析),连接AC与BD交于点O,由正方形的性质可知,![]() ,
,![]() ,设
,设![]() ,在
,在![]() 中,
中,![]() 可求出
可求出![]() ,从而可得DF和BF的长,即可得出答案;
,从而可得DF和BF的长,即可得出答案;
(3)设正方形的边长![]() ,可得DE、AO、BO、BD的长,由
,可得DE、AO、BO、BD的长,由![]() 可得BF的长,又根据
可得BF的长,又根据![]() 可得BG的长,从而可得
可得BG的长,从而可得![]() 的面积
的面积![]() ,用正方形的面积减去三个三角形的面积可得四边形AGCE的面积
,用正方形的面积减去三个三角形的面积可得四边形AGCE的面积![]() ,再利用二次函数的性质求解
,再利用二次函数的性质求解![]() 的最大值.
的最大值.
(1)![]() 为CD中点,
为CD中点,![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() ,即
,即![]()
又![]()
![]() ;
;
(2)如图,连接AC与BD交于点O
由正方形的性质得![]() ,
,![]()
设![]()
在![]() 中,
中,![]()
![]()
![]() ,
,![]()
![]() ;
;
(3)设正方形的边长![]() ,则
,则![]()
![]()
![]()
![]()
由(1)知![]() ,
,![]()
又![]()
![]()
又![]()
![]()
![]()
![]()
又![]()
![]()
![]()
![]()
由二次函数图象的性质得:当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() .
.



 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图矩形![]() 是矩形ABCD的“减半”矩形.
是矩形ABCD的“减半”矩形.
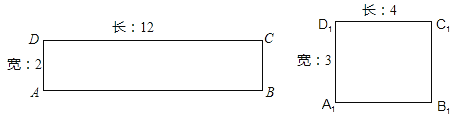
请你解决下列问题:
(1)当矩形的长和宽分别为1,2时,它是否存在“减半”矩形?请作出判断,并请说明理由;
(2)边长为![]() 的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知抛物线![]() (b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,﹣1),C的坐标为(4,3),直角顶点B在第四象限.
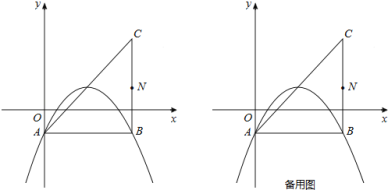
(1)如图,若该抛物线过A,B两点,求该抛物线的函数表达式;
(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与AC交于另一点Q.
(i)若点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M、P、Q三点为顶点的三角形是等腰直角三角形时,求出所有符合条件的点M的坐标;
(ii)取BC的中点N,连接NP,BQ.试探究![]() 是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
是否存在最大值?若存在,求出该最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,解决问题:
材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末两位、末三位、末四位即可,推广成一条结论;末![]() 位能被
位能被![]() 整除的数,本身必能被
整除的数,本身必能被![]() 整除,反过来,末
整除,反过来,末![]() 位不能被
位不能被![]() 整除的数,本身也不可能被
整除的数,本身也不可能被![]() 整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
整除,例如判断992250能否被25、625整除时,可按下列步骤计算:
![]() ,
,![]() 为整数,
为整数,![]() 能被25整除
能被25整除
![]() ,
,![]() 不为整数,
不为整数,![]() 不能被625整除
不能被625整除
材料2:用奇偶位差法判断一个数能否被11这个数整除时,可把这个数的奇位上的数字与偶位上的数字分别加起来,再求它们的差,看差能否被11整除,若差能被11整除,则原数能被11整除,反之则不能.
(1)若![]() 这个三位数能被11整除,则
这个三位数能被11整除,则![]() ;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
;在该三位数末尾加上和为8的两个数字,让其成为一个五位数,该五位数仍能被11整除,求这个五位数
(2)若一个六位数p的最高位数字为5,千位数字是个位数字的2倍,且这个数既能被125整除,又能被11整除,求这个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
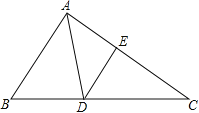
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0),B(3,0)两点.
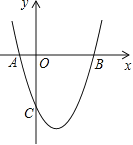
(1)求该抛物线的解析式;
(2)求该抛物线的对称轴以及顶点坐标;
(3)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=8,并求出此时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
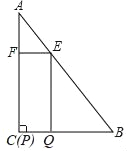
【题目】如图,在△ABC中,∠A=30°,∠C=90°,AB=12,四边形EFPQ是矩形,点P与点C重合,点Q、E、F分别在BC、AB、AC上(点E与点A、点B均不重合).
(1)当AE=8时,求EF的长;
(2)设AE=x,矩形EFPQ的面积为y.
①求y与x的函数关系式;
②当x为何值时,y有最大值,最大值是多少?
(3)当矩形EFPQ的面积最大时,将矩形EFPQ以每秒1个单位的速度沿射线CB匀速向右运动(当点P到达点B时停止运动),设运动时间为t秒,矩形EFPQ与△ABC重叠部分的面积为S,求S与t的函数关系式,并写出t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y= x2-4x+3.
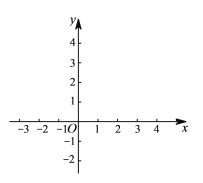
(1)把这个二次函数化成![]() 的形式并写出抛物线的顶点坐标;
的形式并写出抛物线的顶点坐标;
(2)画出这个二次函数的图象,并利用图象直接写出当y>0时,x的取值范围. 当x取何值时,y随x的增大而减小;
(3)若抛物线与![]() 轴的交点记为A,B,该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
轴的交点记为A,B,该图象上存在一点C,且△ABC的面积为3,求点C的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com