
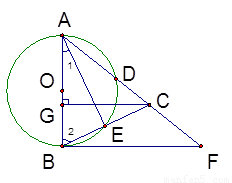
如图,在△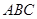 中,
中,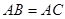 ,以
,以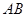 为直径的⊙O分别交
为直径的⊙O分别交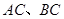 于点
于点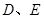 , 点
, 点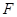 在
在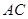 的延长线上,且
的延长线上,且 ∠
∠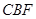
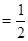 ∠
∠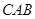 。
。

1.(1) 求证:AB⊥BF
2.(2) 若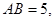 sin∠CBF=
sin∠CBF=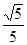 , 求BC和BF的长。
, 求BC和BF的长。
1.(1)证明:连结AE.
∵AB是⊙O的直径,
∴∠AEB=90º
∴∠1+∠2=90º
∵AB=AC
∴∠1= ∠CAB
∠CAB
∵∠CBF= ∠CAB
∠CAB
∴∠1=∠CBF
∴∠CBF+∠2=90º
即∠ABF=90º
∴AB⊥BF …………2分
2.(2) 解:过点C作CG⊥AB于点G.
∵sin∠CBF= ,∠1=∠CBF,
,∠1=∠CBF,
∴sin∠1= ,
,
∵∠AEB=90º,AB=5,
∴BE=AB·sin∠1= ,
,
∵AB=AC, ∠AEB=90º,
∴BC=2BE=2
在Rt△ABE中,由勾股定理得AE=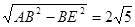
∴sin∠2= ,cos∠2=
,cos∠2= .
.
在Rt△CBG中,可求得 GC=4,GB=2
∴AG=3.
∵GC∥BF,
∴△AGC∽△ABF
∴ ∴BF=
∴BF= …………5分
…………5分
【解析】略


科目:初中数学 来源: 题型:
(本题满分12分)
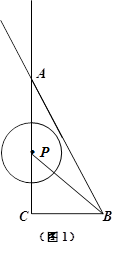
如图,在△ACB中,∠ACB = 90°,AC = 4,BC = 2,点P为射线CA上的一个动点,以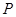 为圆心,1为半径作
为圆心,1为半径作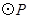 .
.
(1)连结 ,若
,若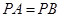 ,试判断
,试判断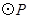 与直线AB的位置关系,并说明理由;
与直线AB的位置关系,并说明理由;
(2)当PC为 时,![]() 与直线AB相切?当
与直线AB相切?当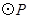 与直线AB相交时,写出PC的取值范围为 ;
与直线AB相交时,写出PC的取值范围为 ;
(3)当![]() 与直线AB相交于点M、N时,是否存在△PMN为正三角形?若存在,求出PC的值;若不存在,说明理由.
与直线AB相交于点M、N时,是否存在△PMN为正三角形?若存在,求出PC的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
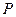 为圆心,1为半径作
为圆心,1为半径作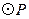 .
. ,若
,若 ,试判断
,试判断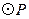 与直线AB的位置关系,并说明理由;
与直线AB的位置关系,并说明理由;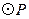 与直线AB相切?当
与直线AB相切?当 与直线AB相交时,写出PC的取值范围为 ;
与直线AB相交时,写出PC的取值范围为 ; 与直线AB相交于点M、N时,是否存在△PMN为正三角形?若存在,求出PC的值;若不存在,说明理由.
与直线AB相交于点M、N时,是否存在△PMN为正三角形?若存在,求出PC的值;若不存在,说明理由.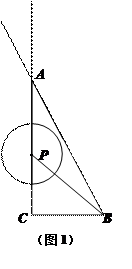
查看答案和解析>>
科目:初中数学 来源:2013届江苏扬州江都区九年级网上阅卷适应性调研考试数学试卷(带解析) 题型:解答题
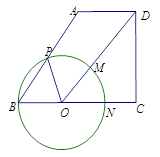
如图,在梯形 中
中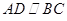 ,
,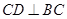 ,已知
,已知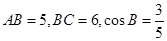 ,点
,点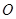 为
为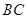 边上的动点,连接
边上的动点,连接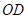 ,以
,以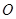 为圆心,
为圆心,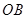 为半径的⊙
为半径的⊙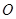 分别交射线
分别交射线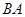 于点
于点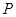 ,交射线
,交射线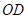 于点
于点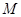 ,交射线
,交射线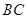 于
于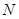 ,连接
,连接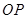 .
.
(1)求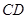 的长.
的长.
(2)当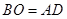 时,求
时,求 的长.
的长.
(3)在点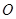 的运动过程中,
的运动过程中,
①当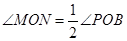 时,求⊙
时,求⊙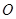 的半径.
的半径.
②当 时,求⊙
时,求⊙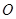 的半径(直接写出答案).
的半径(直接写出答案).
查看答案和解析>>
科目:初中数学 来源:2012-2013学年广西贵港市平南县九年级5月第二次模拟考试数学试卷(解析版) 题型:解答题
如图,在扇形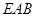 中,半径长
中,半径长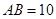 ,
, ;以
;以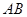 为直径作半圆
为直径作半圆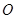 ,点
,点 是弧
是弧 上的一个动点,
上的一个动点,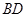 与半圆
与半圆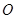 交于点
交于点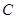 ,
,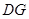 ⊥
⊥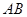 于点
于点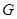 ,
,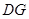 与
与 交于点
交于点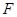 ,连结
,连结 .
.

(1)求证: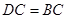 ;
;
(2)设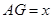 ,
, 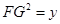 ,试求
,试求 关于
关于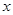 的函数关系式,并写出
的函数关系式,并写出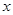 的取值范围;
的取值范围;
(3)若点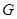 落在线段
落在线段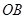 上,当
上,当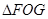 ∽
∽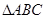 时,求线段
时,求线段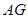 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源:2012-2013学年江苏省扬州市中考一模数学试卷(解析版) 题型:解答题
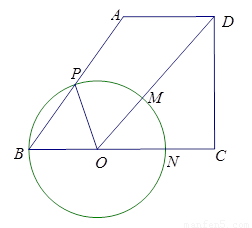
如图,在梯形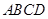 中
中 ,
, ,已知
,已知 ,点
,点 为
为 边上的动点,连接
边上的动点,连接 ,以
,以 为圆心,
为圆心,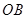 为半径的⊙
为半径的⊙ 分别交射线
分别交射线 于点
于点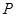 ,交射线
,交射线 于点
于点 ,交射线
,交射线 于
于 ,连接
,连接 .
.
(1)求 的长.
的长.
(2)当 时,求
时,求 的长.
的长.
(3)在点 的运动过程中,
的运动过程中,
①当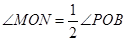 时,求⊙
时,求⊙ 的半径.
的半径.
②当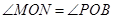 时,求⊙
时,求⊙ 的半径(直接写出答案).
的半径(直接写出答案).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com