
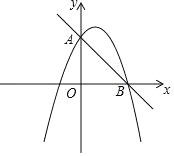
【题目】如图,直线y=﹣x+4与抛物线y=﹣![]() x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.
(1)求抛物线的解析式;
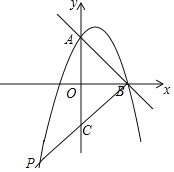
(2)在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;
(3)点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+x+4;(2)P(-4,-8);(3)存在,点F的坐标为(5,
x2+x+4;(2)P(-4,-8);(3)存在,点F的坐标为(5,![]() ),(﹣3,
),(﹣3,![]() ),(3,
),(3,![]() ).
).
【解析】
(1)由直线表达式求出点A、B的坐标,把A、B点坐标代入二次函数表达式,即可求解;
(2)OA=OB=4,则OB为AC的垂直平分线,则点C坐标为(0,-4),求出直线BC的表达式,即可求解;
(3)存在;分OB是平行四边形的一条边或一条对角线两种情况,分别求解即可.
解:(1)在y=﹣x+4中,
当x=0时, y=4,当y=0时,x=4,
即点A、B的坐标分别为(0,4)、(4,0),
将(0,4)、(4,0),代入二次函数表达式,并解得:
b=1,c=4,
抛物线的解析式为:y=﹣![]() x2+x+4;
x2+x+4;
(2)∵OA=OB=4,
∴∠ABO=45°,
∵∠ABP=90°,
则∠PBO=45°,
若直线PB交y轴于点M,
则OM=OB=4,
可得直线BP的解析式为:y=x-4,
联立:y=x-4,y=﹣![]() x2+x+4,得:
x2+x+4,得:
x=4,y=0(即B点);x=-4,y=-8,
即P(-4,-8);
(3)存在;
由y=﹣![]() x2+x+4知抛物线的对称轴为:x=1,
x2+x+4知抛物线的对称轴为:x=1,
设E(1,m),F(n,﹣![]() n2+n+4),O(0,0),B(4,0),
n2+n+4),O(0,0),B(4,0),
①当四边形OBEF是平行四边形时,
有:EF=4,
∴n-1=-4,即n=-3,
F点坐标为(-3,![]() );
);
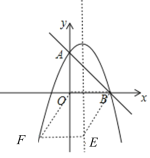
②当四边形OBFE是平行四边形时,
有:EF=4,
n-1=4,即n=5,
F点坐标为(5,![]() );
);

③当四边形OFBE是平行四边形时,
有: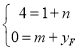 ,
,
即n=3,
F点坐标为(3,![]() );
);
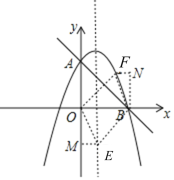
综上所述:点F的坐标为(5,![]() ),(﹣3,
),(﹣3,![]() ),(3,
),(3,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,△ABC为⊙O的内接三角形,AB为⊙O的直径,过点A作⊙O的切线交BC的延长线于点D.
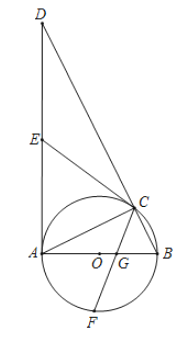
(1)求证:△DAC∽△DBA;
(2)过点C作⊙O的切线CE交AD于点E,求证:CE=![]() AD;
AD;
(3)若点F为直径AB下方半圆的中点,连接CF交AB于点G,且AD=6,AB=3,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
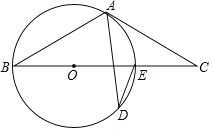
【题目】如图,BE是O的直径,点A和点D是⊙O上的两点,过点A作⊙O的切线交BE延长线于点.
(1)若∠ADE=25°,求∠C的度数;
(2)若AB=AC,CE=2,求⊙O半径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了了解九年级学生“长跑”成绩的情况,随机抽取部分九年级学生,测试其长跑成绩(男子1000米,女子800米),按长跑成绩依次分为A、B、C、D四个等级进行统计.制作如下两个不完整的统计图.
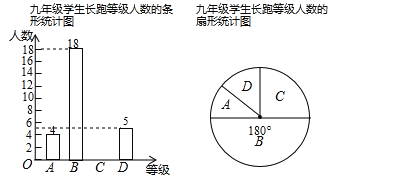
根据所给信息,解答下列问题:
(1)在扇形统计图中,![]() 对应的扇形圆心角是______度;
对应的扇形圆心角是______度;
(2)补全条形统计图;
(3)所抽取学生的“长跑”测试成绩的中位数会落在______等级;
(4)该校九年级有477名学生,请估计“长跑”测试成绩达到![]() 级的学生约有多少人?
级的学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
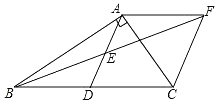
【题目】如图,在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
(1)求证:四边形ADCF是菱形;
(2)若AC=12,AB=16,求菱形ADCF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
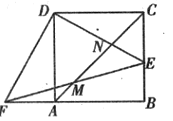
【题目】边长为4的正方形ABCD中,点E是BC边上的一个动点,连接DE,交AC于点N,过点D作DF⊥DE,交BA的延长线于点F,连接EF,交AC于点M.
(1)判定△DFE的形状,并说明理由;
(2)设CE=x,△AMF的面积为y,求y与x之间的函数关系式;并求出当x为何值时y有最大值?最大值是多少?
(3)随着点E在BC边上运动,NA·MC的值是否会发生变化?若不变,请求出NA·MC的值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )
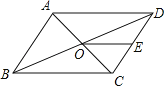
A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com