
如图,在平行四边形ABCD中,∠C=60°,M、N分别是AD、BC的中点,BC=2CD.
(1)求证:四边形MNCD是平行四边形;
(2)求证:BD=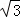 MN.
MN.
科目:初中数学 来源: 题型:
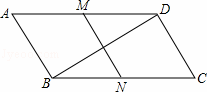
如图,两个连接在一起的菱形的边长都是1cm,一只电子甲虫从点A开始按ABCDAEFGAB…的顺序沿菱形的边循环爬行,当电子甲虫爬行2014cm时停下,则它停的位置是( )
A. 点F B.点E C.点A D. 点C
查看答案和解析>>
科目:初中数学 来源: 题型:
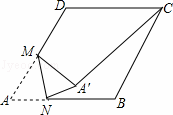
如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线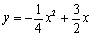 .
.
(Ⅰ)求它的对称轴与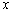 轴交点
轴交点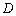 的坐标;
的坐标;
(Ⅱ)将该抛物线沿它的对称轴向上平移,设平移后的抛物线与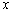 轴的交点为
轴的交点为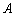 ,
,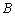 ,与
,与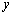 轴的交点为
轴的交点为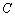 ,若
,若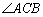 =90°,求此时抛物线的解析式;
=90°,求此时抛物线的解析式;
(Ⅲ)若点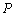 (
(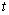 ,
,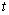 )在抛物线上,则称点
)在抛物线上,则称点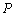 为
为 抛物线的
抛物线的 不动点.将抛物线
不动点.将抛物线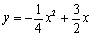 进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线
进行平移,使其只有一个不动点,此时抛物线的顶点是否在直线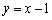 上,请说明理由.
上,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
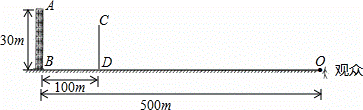
如图假设一座大楼高30米,观众坐在距大楼500米处,魔术师只需做一个屏障,屏障上的图画和没有大楼以后的景物一样,将屏障立在大楼前100米处,这样观众看上去好像大楼突然消失了.若要完全挡住大楼,请你找到一个方法计算出屏障至少要多高?(人身高忽略不计)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com