
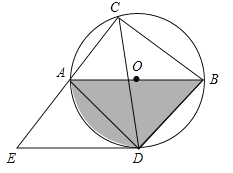
【题目】如图,⊙O的直径AB=10,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的曲边三角形的面积是 ;
围成的曲边三角形的面积是 ;
(2)求证:DE是⊙O的切线;
(3)求线段DE的长.
【答案】(1)![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)连接OD,由AB是直径知∠ACB=90°,结合CD平分∠ACB知∠ABD=∠ACD=45°,从而知∠AOD=90°,根据曲边三角形的面积=S扇形AOD+S△BOD可得答案;
(2)由∠AOD=90°,即OD⊥AB,根据DE∥AB可得OD⊥DE,即可得证;
(3)勾股定理求得BC=8,作AF⊥DE知四边形AODF是正方形,即可得DF=5,由∠EAF=90°﹣∠CAB=∠ABC知tan∠EAF=tan∠CBA,即![]() ,求得EF的长即可得.
,求得EF的长即可得.
解:(1)如图,连接OD.∵AB是直径,且AB=10,
∴∠ACB=90°,AO=BO=DO=5.
∵CD平分∠ACB,∴∠ABD=∠ACD=![]() ∠ACB=45°,
∠ACB=45°,
∴∠AOD=90°,则曲边三角形的面积是
S扇形AOD+S△BOD=![]() +
+![]() ×5×5=
×5×5=![]() .
.
故答案为![]() ;
;
(2)由(1)知∠AOD=90°,即OD⊥AB.
∵DE∥AB,∴OD⊥DE,
∴DE是⊙O的切线;
(3)∵AB=10、AC=6,∴BC=![]() =8.
=8.
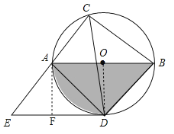
过点A作AF⊥DE于点F,则四边形AODF是正方形,∴AF=OD=FD=5,∴∠EAF=90°﹣∠CAB=∠ABC,
∴tan∠EAF=tan∠CBA,
∴![]() ,即
,即![]() ,
,
∴EF=![]() ,
,
∴DE=DF+EF=![]() +5=
+5=![]() .
.


 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】(2014广州)从广州到某市,可乘坐普通列车或高铁,已知高铁的行驶路程是400千米,普通列车的行驶路程是高铁的行驶路程的1.3倍.
(1)求普通列车的行驶路程;
(2)若高铁的平均速度(千米/时)是普通列车平均速度(千米/时)的2.5倍,且乘坐高铁所需要时间比乘坐普通列车所需时间缩短3小时,求高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”期间甲乙两商场搞促销活动,甲商场的方案是:在一个不透明的箱子里放4个完全相同的小球,球上分别标“0元”“20元”“30元”“50元”,顾客每消费满300元就可从箱子里不放回地摸出2个球,根据两个小球所标金额之和可获相应价格的礼品;乙商场的方案是:在一个不透明的箱子里放2个完全相同的小球,球上分别标“5元”“30元”,顾客每消费满100元,就可从箱子里有放回地摸出1个球,根据小球所标金额可获相应价格的礼品.某顾客准备消费300元.
(1)请用画树状图或列表法,求出该顾客在甲商场获得礼品的总价值不低于50元的概率;
(2)判断该顾客去哪个商场消费使获得礼品的总价值不低于50元机会更大?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】国家为了推进教育均衡发展,在乡镇中心学校开设的体育选修课有A﹣篮球,B﹣足球,C﹣排球,D﹣羽毛球,E﹣乒乓球,学生可根据自己的爱好选修一门,学校张老师对某班全班同学的选课情况进行调查统计,制成了两幅不完整的统计图(如图):
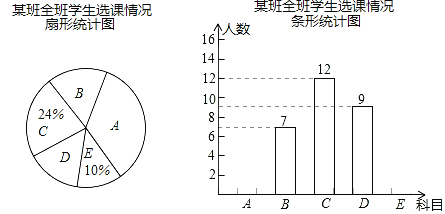
(1)求出该班的总人数,并补全条形统计图;
(2)求出“足球”在扇形统计图中的圆心角是多少度;
(3)若该班所在的年级共有1200人,请估计选篮球的学生有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的边AB=20,面积为320,∠BAD<90°,⊙O与边AB,AD都相切,AO=10,则⊙O的半径长等于( )
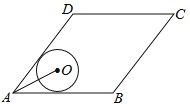
A.5 B.6 C.2![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如今很多初中生喜欢购买饮品饮用,既影响身体健康又给家庭增加不必要的开销,为此某班数学兴趣小组对本班同学一天饮用饮品的情况进行了调查,大致可分为四种:A:白开水,B:瓶装矿泉水,C:碳酸饮料,D:非碳酸饮料,根据统计结果绘制如下两个不完整的统计图,根据统计图提供的信息,解答下列问题:
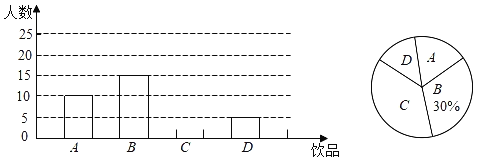
(1)这个班级有 名同学;并补全条形统计图;
(2)若该班同学每人每天只饮用一种饮品(每种仅限一瓶,价格如表),则该班同学每天用于饮品的人均花费是多少元?

(3)在饮用白开水的同学中有4名班委干部,为了养成良好的生活习惯,班主任决定在这4名班委干部(其中有两位班长记为A,B,其余两位记为C,D)中随机抽取2名作为良好习惯监督员,请用列表法或画树状图的方法,求出恰好抽到2名班长的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”期间,老张在某商场购物后,参加了出口处的抽奖活动.抽奖规则如下:每张发票可摸球一次,每次从装有大小形状都相同的1个白球和2个红球的盒子中,随机摸出一个球,若摸出的是白球,则获得一份奖品;若摸出的是红球,则不获奖.
(1)求每次摸球中奖的概率;
(2)老张想“我手中有两张发票,那么中奖的概率就翻了一倍.”你认为老张的想法正确吗?用列表法或画树形图分析说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
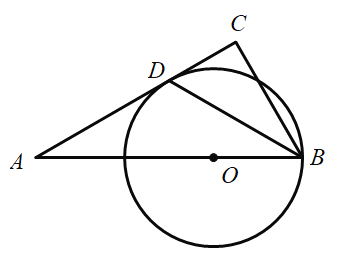
【题目】如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半轻的⊙O与AC相切于点D,BD平分∠ABC,∠ABC=60°.
(1)求∠C的度数;
(2)若圆的半径OB=2,求线段CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(0,1),B(3,3) ,C(1,3) .

(1)画出△ABC关于点O的中心对称图形△A1B1C1;
(2)画出△ABC绕点A逆时针旋转90![]() 的△AB2C2;直接写出点C2的坐标为 ;
的△AB2C2;直接写出点C2的坐标为 ;
(3)求在△ABC旋转到△AB2C2的过程中,点C所经过的路径长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com