
| A. | 这50名考生是总体的一个样本 | B. | 近1千名考生是总体 | ||
| C. | 每位考生的数学成绩是个体 | D. | 50名学生是样本容量 |
分析 总体是指考查的对象的全体,个体是总体中的每一个考查的对象,样本是总体中所抽取的一部分个体,而样本容量则是指样本中个体的数目.我们在区分总体、个体、样本、样本容量,这四个概念时,首先找出考查的对象.从而找出总体、个体.再根据被收集数据的这一部分对象找出样本,最后再根据样本确定出样本容量.
解答 解:A、这50名考生的数学成绩是总体的一个样本,故选项错误;
B、近1千名考生的数学成绩是总体,故选项错误;
C、每位考生的数学成绩是个体,正确;
D、样本容量是:50,故选项错误;
故选:C.
点评 本题考查了总体、个体、样本和样本容量的定义,解题要分清具体问题中的总体、个体与样本,关键是明确考查的对象.总体、个体与样本的考查对象是相同的,所不同的是范围的大小.样本容量是样本中包含的个体的数目,不能带单位.


科目:初中数学 来源: 题型:选择题
 如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是( )
如图,已知AB、AD是⊙O的弦,∠B=30°,点C在弦AB上,连接CO并延长CO交于⊙O于点D,∠D=20°,则∠BAD的度数是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
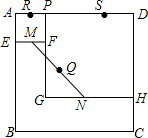 如图,四边形ABCD是边长为8的正方形,点R、S在边AD上,且AR=1,SD=2,点P是线段RS上的动点,分别以AP、PD为边在正方形ABCD内作正方形AEFP和PGHD,M、N分别为EF、GH的中点.连结MN,设MN的中点为0,则当点P从点R运动到点S时,点O移动的路径长为2.5.
如图,四边形ABCD是边长为8的正方形,点R、S在边AD上,且AR=1,SD=2,点P是线段RS上的动点,分别以AP、PD为边在正方形ABCD内作正方形AEFP和PGHD,M、N分别为EF、GH的中点.连结MN,设MN的中点为0,则当点P从点R运动到点S时,点O移动的路径长为2.5.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com