Question

6．在△ABC中，∠A=90°，AC=5，AB=12，将△ABC放在如图所示的平面直角坐标系中，且点B（-8，0）、点C在x在轴上，P是y正半轴上一动点，把△POC绕点C逆时针旋转∠ACB的度数，点P旋转后的对应点为Q．
（1）若OP=2时，则Q点的坐标是（$\frac{16}{13}$，-$\frac{50}{13}$）．（直接写出结果）
（2）若旋转后所得三角形和△ABC相似时，求此时点Q的坐标；
（3）是否存在满足条件的点P，使直线PQ恰好过点M（-6，3）；若存在，求出点P的坐标，若不存在，请说明理由．

Answer 1

分析 （1）如图1，延长CP交AB于M，作QN⊥OC于N．求出直线PA、CM的解析式，解方程组求出点M坐标，求出AM、CM，再利用△CAM∽△CNQ，得$\frac{CA}{CN}$=$\frac{AM}{NQ}$=$\frac{CM}{CQ}$，求出NQ、CN即可解决问题．
（2）分两种情形）①如图2中，当△PCO∽△CBA时满足条件，此时易知CQ=PC=$\frac{65}{12}$，∠MBC=∠MCB，设BM=MC=x，在RtAMC中，利用勾股定理求出x，再利用由△CAM∽△CNQ，可得$\frac{CA}{CN}$=$\frac{AM}{NQ}$=$\frac{CM}{CQ}$，即可解决问题．②如图3中，若△CPO∽△CBA时，此时△CPO≌△CBA，点Q恰好与点B重合，所以Q（-8，0）．
（3）设点P的坐标为（t，0），同法可得Q的坐标是（$\frac{40-12t}{13}$，$\frac{5t-60}{13}$），设y=kx+b过（-6，3），（0，t），可得y=$\frac{t-3}{6}$x+t，把（$\frac{40-12t}{13}$，$\frac{5t-60}{13}$），代入y=$\frac{t-3}{6}$x+t解方程即可．

解答 （1）解：如图1，延长CP交AB于M，作QN⊥OC于N．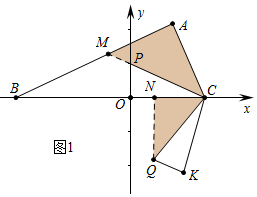

∵∠ACB=∠PCQ，
∴∠ACM=∠NCO，∵∠A=∠QNC=90°，
∴△CAM∽△CNQ，
∴$\frac{CA}{CN}$=$\frac{AM}{NQ}$=$\frac{CM}{CQ}$，
由题意B（-8，0），A（$\frac{40}{13}$，$\frac{60}{13}$），
∴直线AB的解析式为y=$\frac{5}{12}$x+$\frac{10}{3}$，
∵C（5，0），P（0，2），
∴直线CP的解析式为y=-$\frac{2}{5}$x+2，
由$\left\{\begin{array}{l}{y=-\frac{2}{5}x+2}\\{y=\frac{5}{12}x+\frac{10}{3}}\end{array}\right.$解得$\left\{\begin{array}{l}{x=-\frac{80}{49}}\\{y=\frac{130}{49}}\end{array}\right.$，
∴M（-$\frac{80}{49}$，$\frac{130}{49}$），
∴AM=$\sqrt{（\frac{40}{13}+\frac{80}{49}）^{2}+（\frac{60}{13}-\frac{130}{49}）^{2}}$=$\frac{250}{49}$，MC=$\sqrt{（5+\frac{80}{49}）^{2}+（\frac{130}{49}）^{2}}$=$\frac{65}{49}$$\sqrt{29}$，
∴$\frac{5}{CN}$=$\frac{\frac{250}{49}}{NQ}$=$\frac{\frac{65\sqrt{29}}{49}}{\sqrt{29}}$，
∴CN=$\frac{49}{13}$，NQ=$\frac{50}{13}$，
∴ON=$\frac{16}{13}$，
∴Q（$\frac{16}{13}$，-$\frac{50}{13}$）．
故答案是：（$\frac{16}{13}$，-$\frac{50}{13}$）．

（2）①如图2中，当△PCO∽△CBA时满足条件，此时易知CQ=PC=$\frac{65}{12}$，∠MBC=∠MCB，设BM=MC=x，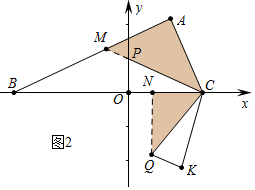

在Rt△AMC中，∵AM²+AC²=CM²，
∴（12-x）²+5²=x²，
∴x=$\frac{169}{24}$，
∴CM=AM=$\frac{169}{24}$，AM=$\frac{119}{24}$，
由△CAM∽△CNQ，可得$\frac{CA}{CN}$=$\frac{AM}{NQ}$=$\frac{CM}{CQ}$，
∴NQ=$\frac{595}{156}$，CN=$\frac{50}{13}$，
∴ON=$\frac{15}{13}$，
∴点Q坐标（$\frac{15}{13}$，-$\frac{595}{156}$）．
②如图3中，若△CPO∽△CBA时，此时△CPO≌△CBA，点Q恰好与点B重合，所以Q（-8，0），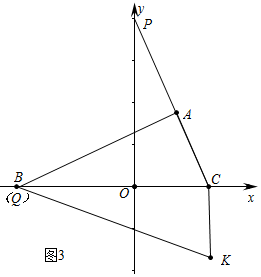

综上所述，点Q的坐标是（$\frac{15}{13}$，-$\frac{595}{156}$）．

（3）设点P的坐标为（t，0），同法可得Q的坐标是（$\frac{40-12t}{13}$，$\frac{5t-60}{13}$），
设y=kx+b过（-6，3），（0，t），则有$\left\{\begin{array}{l}{-6k+b=3}\\{b=t}\end{array}\right.$，解得k=$\frac{t-3}{6}$
∴y=$\frac{t-3}{6}$x+t，
把（$\frac{40-12t}{13}$，$\frac{5t-60}{13}$），代入y=$\frac{t-3}{6}$x+t，
化简得3t²-31t-120=0，解得t=12，t=-$\frac{5}{3}$ （不合题意，舍去），
∴点P的坐标是（0，12）．

点评 本题考查相似综合题、一次函数、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会分类讨论的思想思考问题，学会用方程组求两个函数图象交点坐标，属于中考压轴题．