


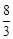 );(2)
);(2)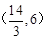 ,
,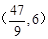 ,
,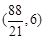 .
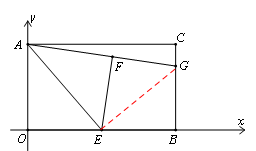
. 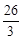 ,在Rt△ABM中,由勾股定理可得CG=
,在Rt△ABM中,由勾股定理可得CG=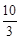 ,从而BG=
,从而BG=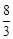 ,得到G的坐标为(8,
,得到G的坐标为(8,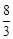 );(2)分点C为黄金圆的圆心,点P为黄金圆的圆心,点Q为黄金圆的圆心三种情况讨论即可.
);(2)分点C为黄金圆的圆心,点P为黄金圆的圆心,点Q为黄金圆的圆心三种情况讨论即可.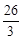 .
.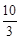 ,∴BG=
,∴BG=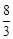 .
.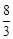 ) .
) .
 ,此时CP=
,此时CP= ,AP=
,AP=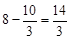 ,P点坐标为
,P点坐标为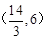 .
. CQ=
CQ=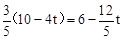 ,PE=
,PE=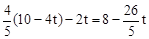 ,
,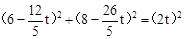 ,
,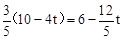 化简得:
化简得: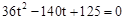 ,
,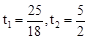 (舍去).
(舍去). ,P点坐标为
,P点坐标为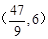 .
. ,PF=
,PF=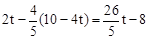 ,
, ,整理得
,整理得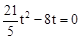 .
. (舍去).
(舍去).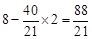 ,P点坐标为
,P点坐标为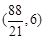 .
.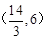 ,
,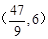 ,
,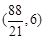 .
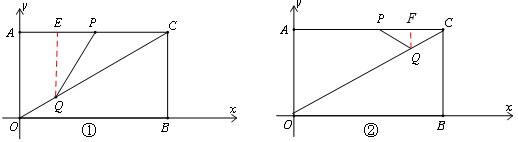
.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:初中数学 来源:不详 题型:解答题
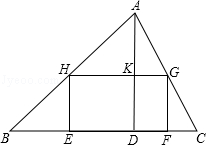
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
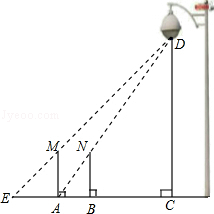
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

A. | B. | C. | D. |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com