
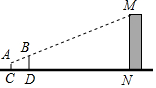
 小亮想借助标杆测量教学楼的高度,他采用了下面的方法,先在楼前距离点N57m处直立一根高2m的标杆BD,然后他往后退,退到距离标杆3m的C处(点C,D,N在一条直线上)蹲下,通过调整眼睛离地面的高度,当楼的顶部M,标杆的顶部B及他的眼睛A恰好在同一条直线上时,让同伴量出眼睛与地面的距离AC为1m,根据上面的数据.你能帮小亮求出教学楼的高度吗?
小亮想借助标杆测量教学楼的高度,他采用了下面的方法,先在楼前距离点N57m处直立一根高2m的标杆BD,然后他往后退,退到距离标杆3m的C处(点C,D,N在一条直线上)蹲下,通过调整眼睛离地面的高度,当楼的顶部M,标杆的顶部B及他的眼睛A恰好在同一条直线上时,让同伴量出眼睛与地面的距离AC为1m,根据上面的数据.你能帮小亮求出教学楼的高度吗? 分析 先过点A作AF⊥MN于点F,交BD于点E,可以构造矩形,利用平行线分线段成比例定理的推论易得△ABE∽△AMF,再利用比例线段,可求MF,进而可求MN.
解答 解:如图,过点A作AF⊥MN于点F,交BD于点E,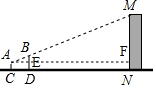
由题意知,AE=CD=3,EF=DN=57,AC=ED=FN=1,
∴BE=BD-DE=1,
∵BE∥MF,
∴△ABE∽△AMF,
∴$\frac{BE}{MF}=\frac{AE}{AE+EF}$,即$\frac{1}{MF}=\frac{3}{3+57}$,
解得:MF=20,
∴MN=MF+FN=21,
答:教学楼的高度为21m.
点评 本题考查了相似三角形的判定和性质,解题的关键是利用平行线分线段成比例定理的推论得出△ABE∽△AMF.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2a与-3b是同类项 | B. | 0.5x3y2和7x2y3是同类项 | ||
| C. | -a3b2和$\frac{4}{3}$b2a3是同类项 | D. | $\frac{2}{3}$xyz与$\frac{2}{3}$xy是同类项 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 多项式5x2+4x-2的项是5x2,4x,-2 | B. | 多项式x2-2x+3是二次三项式 | ||
| C. | 2×3,$\frac{a+b}{3}$,$\frac{ab}{2}$,$\frac{3a}{π}$都是单项式 | D. | 3-4a中,一次项的系数是-4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
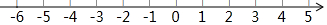 已知关于x的多项式(a+5)x|a|-3+3x-3是二次三项式,一次项系数为b,常数项为c,且a、b、c分别是点A、B、C在数轴上对应的数.
已知关于x的多项式(a+5)x|a|-3+3x-3是二次三项式,一次项系数为b,常数项为c,且a、b、c分别是点A、B、C在数轴上对应的数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com