
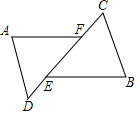
 如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由.
如图所示,△ADF和△BCE中,∠A=∠B,点D,E,F,C在同一直线上,有如下三个关系式:①AD=BC;②DE=CF;③BE∥AF.请用其中两个关系式作为条件,另一个作为结论,写出的一个正确结论,并说明它正确的理由. 科目:初中数学 来源: 题型:解答题
 如图,已知直线y=$\frac{1}{3}$x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.
如图,已知直线y=$\frac{1}{3}$x+1与x轴交于点A,与y轴交于点B,将△AOB绕点O顺时针旋转90°后得到△COD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 时间t/天 | 1 | 3 | 6 | 10 | 20 | 40 | … |
| 日销售量y/千克 | 118 | 114 | 108 | 100 | 80 | 40 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com