
【题目】探究:如图①,在△ABC 中,∠BAC=90°,AB=AC,直线 m 经过点 A,BD⊥m 于点 D,CE⊥m 于点 E,求证:△ABD≌△CAE.
应用:如图②,在△ABC 中,AB=AC,D、A、E 三点都在直线 m 上,并且有∠BDA=∠AEC=∠BAC,求证:DE=BD+CE.

【答案】证明见解析
【解析】
(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90![]() ,而∠BAC=90
,而∠BAC=90![]() ,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA.则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA.则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;
(2)利用∠BDA=∠BAC=α,则∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,得出∠CAE=∠ABD,进而得出△ADB≌△CEA即可得出答案.
证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
 ,
,
∴△ADB≌△CEA(AAS);
(2)设∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
【题目】某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个,2个甲种部件和3个乙种部件配成一套,问加工甲、乙两种部件各安排多少人才能使每天加工的两种部件刚好配套?并求出加工了多少套?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尝试探究并解答:
(1)为了求代数式x2+2x+3的值,我们必须知道x的值,若x=1,则这个代数式的值为 ;若x=2,则这个代数式的值为 ,可见,这个代数式的值因x的取值不同而 (填“变化”或“不变”).尽管如此,我们还是有办法来考虑这个代数式的值的范围.
(2)本学期我们学习了形如a2+2ab+b2及a2﹣2ab+b2的式子,我们把这样的多项式叫做“完全平方式”在运用完全平方公式进行因式分解时,关键是判断这个多项式是不是一个完全平方式同样地,把一个多项式进行部分因式分解可以解决代数式的最大(或最小)值问题例如:x2+2x+3=(x2+2x+1)+2=(x+1)2+2,因为(x+1)2≥0,所以(x+1)2+2≥2,所以这个代数式x2+2x+3有最小值是2,这时相应的x的值是 .
(3)猜想:①4x2﹣12x+13的最小值是 ;
②﹣x2﹣2x+3有 值(填“最大”或“最小”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学著作《九章算术》中有这样一道题,原文是:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步(两人的步长相同).走路慢的人先走100步,走路快的人要走多少步才能追上走路慢的人(两人走的路线相同)?试求解这个问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的例题,再解答后面的题目.
例:已知x2+y2﹣2x+4y+5=0,求x+y的值.
解:由已知得(x2﹣2x+1)+(y2+4y+4)=0,
即(x﹣1)2+(y+2)2=0.
因为(x﹣1)2≥0,(y+2)2≥0,它们的和为0,
所以必有(x﹣1)2=0,(y+2)2=0,
所以x=1,y=﹣2.
所以x+y=﹣1.
题目:已知x2+4y2﹣6x+4y+10=0,求xy的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD为⊙O的直径,弦AB交CD于点E,连接BD、OB. 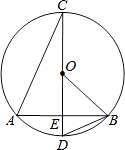
(1)求证:△AEC∽△DEB;
(2)若CD⊥AB,AB=8,DE=2,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分:
类别 | A | B | C | D | E |
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 12 | 30 |
| 54 | 9 |

根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有多少人,这些学生数占被调查总人数的百分比为多少;
(2)被调查学生的总人数为多少人,统计表中![]() 的值为多少,统计图中
的值为多少,统计图中![]() 的值为多少;
的值为多少;
(3)求在统计图中,B类所对应扇形圆心角的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com