
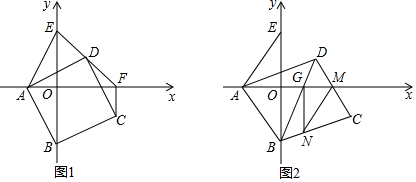
分析 (1)取中点,构建中位线DH,证明△ABO≌△DAH≌△AEO,得出AH=2DH,设DH=x,则AH=2x,
由勾股定理列方程求出x的值,写出A、E的坐标;
(2)根据等腰三角形三线合一的性质得:OD⊥EF,根据SAS证明△ADO≌△CDF,则FC=AO=2$\sqrt{5}$;
(3)作辅助线,构建垂线和全等三角形,先根据角平分线的性质得:GK=GQ,证明△AKG≌△NQG,则AG=NG,所以∠GAN=45°,再证明△PAN≌△MAN,可得结论.
解答 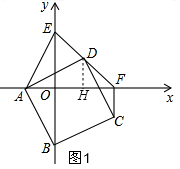 解:(1)如图1,取OF的中点H,连接DH,
解:(1)如图1,取OF的中点H,连接DH,
∵D为EF的中点,
∴DH是△OEF的中位线,
∴DH∥OE,
∴∠DHA=∠EOA=90°,
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴∠BAO+∠OAD=90°,
∵∠OAD+∠ADH=90°,
∴∠BAD=∠ADH,
∴△ABO≌△DAH,
∵E、B关于x轴对称,
∴△AOE≌△AOB,
∴△ABO≌△DAH≌△AEO,
∴AO=DH,OB=OE=AH,
∵OE=OF,∠EOF=90°,
∴△EOF是等腰直角三角形,
∴∠DFO=45°,
∴△DHF是等腰直角三角形,
∴DH=FH,
∴DH=FH=OH,
∴DH=AO=OH,
∴AH=2DH,
设DH=x,则AH=2x,
由勾股定理得:x2+(2x)2=102,
5x2=100,
x=±$\sqrt{5}$,
∴AO=2$\sqrt{5}$,EO=2x=4$\sqrt{5}$,
∴A(-2$\sqrt{5}$,0),E(0,4$\sqrt{5}$);
(2)如图2,连接OD,
∵OE=OF,D为EF的中点,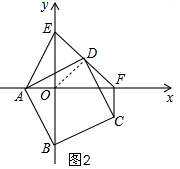
∴OD⊥EF,
∴∠ODF=90°,
∴△ODF为等腰直角三角形,
∴OD=DF,
∵∠ADC=90°,
∴∠ADO=∠FDC,
∵AD=DC,
∴△ADO≌△CDF,
∴FC=AO=2$\sqrt{5}$,
(3)如图3,过G作GK⊥AB于K,过G作GQ⊥BC于Q,连接AN,
∵四边形ABCD为正方形,
∴BD平分∠ABC,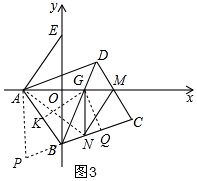
∴GK=GQ,
∵∠KGN+∠NGQ=90°,
∠AGK+∠KGN=90°,
∴∠AGK=∠NGQ,
∵∠AKG=∠NQG=90°,
∴△AKG≌△NQG,
∴AG=NG,
∴∠GAN=45°,
延长NB至点P,使PB=DM,连接AP,
∵AB=AD,∠ABP=∠ADM=90°,
∴△ABP≌△ADM,
∴AP=AM,∠PAB=∠MAD,
∴∠PAN=∠PAB+∠BAN=∠MAD+∠BAN=∠GAN=45°,
∵AN=AN,
∴△PAN≌△MAN,
∴MN=PN=PB+BN=DM+BN.
点评 本题是四边形的综合题,考查了正方形的性质、等腰三角形和等腰直角三角形的性质和判定、全等三角形的性质和判定等,运用的知识较多,在本题中多次构建全等三角形,得出对应线段相等,从面使问题得以解决.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
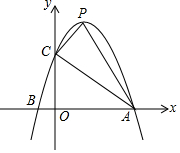 已知抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,顶点为P.
已知抛物线y=-x2+2x+3交x轴于A、B两点,交y轴于C点,顶点为P.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
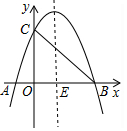 在平面直角坐标系xOy中,已知抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,交y轴于点C.
在平面直角坐标系xOy中,已知抛物线y=-x2+bx+c与x轴交于A(-1,0),B(3,0)两点,交y轴于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com