
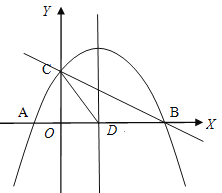
【题目】如图,抛物线![]() 与x轴交于A(-1,0)、B两点, 与y轴交于点C(0,2), 抛物线的对称轴交x轴于点D.
与x轴交于A(-1,0)、B两点, 与y轴交于点C(0,2), 抛物线的对称轴交x轴于点D.
(1)求抛物线的解析式;
(2)求sin∠ABC的值;
(3)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形,如果存在,直接写出点P的坐标;如果不存在,请说明理由;
(4)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时线段EF最长?求出此时E点的坐标.
【答案】(1)解析式为![]() ;
;
(2)![]() ;
;
(3)存在,点P的坐标为(![]() ,
, ![]() )、(
)、(![]() ,4)或(
,4)或(![]() ,-
,-![]() ).
).
(4)当点E坐标为(2,1)时,线段EF最长.
【解析】试题分析: (1)把A(-1,0),C(0,2)代入y=-![]() x2+bx+c列方程组即可.
x2+bx+c列方程组即可.
(2)令y=0,求出x的值,可确定点B的坐标,然后由点B、C的坐标,利用勾股定理可求出BC的长,即可求sin∠ABC的值;
(3)由勾股定理求出CD的值,再以点C为圆心,CD为半径作弧交对称轴于P1,以点D为圆心CD为半径作圆交对称轴于点P2,P3,作CE垂直于对称轴与点E,由等腰三角形的性质及勾股定理就可以求出结论;
(4)设出E点的坐标为(x,-![]() x+2),就可以表示出F的坐标,进而求出EF的长,由二次函数的性质可求出答案.
x+2),就可以表示出F的坐标,进而求出EF的长,由二次函数的性质可求出答案.
试题解析:(1)∵抛物线![]() 过点A(-1,0),C(0,2),
过点A(-1,0),C(0,2),

∴b=![]() ,c=2.
,c=2.
∴解析式为![]() .
.
(2)∵点B的坐标为(4,0),
∴BC=![]() .
.
![]() .
.
(3)存在.
∵点D的坐标为(![]() ,0),
,0),
![]() .
.
∴点P的坐标为(![]() ,
, ![]() )、(
)、(![]() ,4)或(
,4)或(![]() ,-
,- ![]() ).
).
(4)设直线BC的解析式为![]()
∵B、C两点坐标分别为(4,0)、(0,2),
∴4m+n=0,n=2,
∴m=![]() ,n=2
,n=2
∴直线BC的解析式为![]() .
.
设E点坐标为![]() ,则F点坐标为
,则F点坐标为![]()
![]()
∴当点E坐标为(2,1)时,线段EF最长.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】点A(2,﹣3)在反比例函数y= ![]() 的图像上.
的图像上.
(1)试判断点B(﹣1,6),C(﹣3,﹣2)是否在这个反比例函数的图像上,请说明理由;
(2)若P(a﹣1,b),Q(a,c)也在这个反比例函数的图像上,且a<0,试比较b,c的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点C在线段AB上,点M、N分别是AC、BC的中点.![]()
(1)若AC=8cm,CB=6cm,求线段MN的长;
(2)若C为线段AB上任一点,满足AC+CB=a,其它条件不变,你能猜想MN的长度吗?写出你的结论并说明理由;
(3)若C为直线AB上线段AB之外的任一点,且AC=m,CB=n,则线段MN的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1)所示,∠AOB、∠COD都是直角.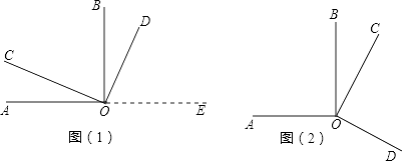
(1)试猜想∠AOD与∠COB在数量上是相等,互余,还是互补的关系.请你用推理的方法说明你的猜想是合理的.
(2)当∠COD绕着点O旋转到图(2)所示位置时,你在(1)中的猜想还成立吗?请你证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解市民“获取新闻的最主要途径”,某市记者开展了一次抽样调查,根据调查结果绘制了如下尚不完整的统计图.
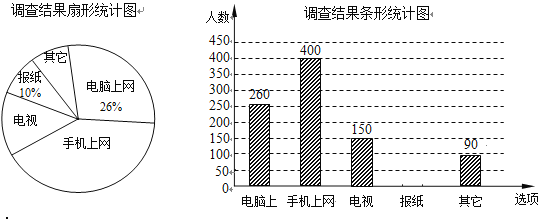
根据以上信息解答下列问题:
(1)这次抽样调查的样本容量是 ;
(2)通过“电视”了解新闻的人数占被调查人数的百分比为 ;扇形统计图中, “手机上网”所对应的圆心角的度数是 ;
(3)请补全条形统计图;
(4)若该市约有70万人,请你估计其中将“电脑和手机上网”作为“获取新闻的最主要途径”的总人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a、b、c满足:① ![]() 与2x2+ay3的和是单项式; ②
与2x2+ay3的和是单项式; ② ![]() ,
,
(1)求a、b、c的值;
(2)求代数式(5b2﹣3c2)﹣3(b2﹣c2)﹣(﹣c2)+2016abc的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ) 
A.带①去
B.带②去
C.带③去
D.带①和②去
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com