
 如图,有一块直角三角形纸片,两直角边AC=7cm,BC=24cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长.
如图,有一块直角三角形纸片,两直角边AC=7cm,BC=24cm,现将直角边AC沿直线AD折叠,使它恰好落在斜边AB上,且与AE重合,求CD的长. 分析 根据折叠的性质可得AC=AE=7cm,CD=DE,∠ACD=∠AED=∠DEB=90°,利用勾股定理列式求出AB,从而求出BE,设CD=DE=x,表示出BD,然后在Rt△DEB中,利用勾股定理列式计算即可得解.
解答 解:∵△ACD与△AED关于AD成轴对称,
∴AC=AE=7cm,CD=DE,∠ACD=∠AED=∠DEB=90°,
在Rt△ABC中,AB2=AC2+BC2=72+242 =252,
∴AB=25,
BE=AB-AE=25-7=18,
设CD=DE=xcm,则DB=BC-CD=24-x,
在Rt△DEB中,由勾股定理,得x2+182=(24-x)2,
解得x=$\frac{21}{4}$,
即CD=$\frac{21}{4}$cm.
点评 本题考查了翻折变换的性质,勾股定理的应用,熟记性质并表示出Rt△DEB的三边,然后利用勾股定理列出方程是解题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
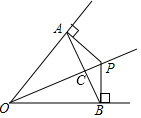 如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:
如图,OP平分∠AOB,PA⊥OA于A,PB⊥OB于B,连结AB交OP于C,给出下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “x2<0(x是实数)”是随机事件 | |
| B. | “打开电视,正在播放《新闻联播》”是必然事件 | |
| C. | “射击运动员射击一次,命中靶心”是随机事件 | |
| D. | “经过由交通信号灯的路口,遇到红灯”是必然事件 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
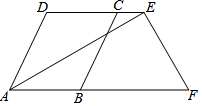 已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,∠DEA=30°,AE⊥EF,垂足为E.
已知如图:AD∥BC,E、F分别在DC、AB延长线上.∠DCB=∠DAB,∠DEA=30°,AE⊥EF,垂足为E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 大瓶 | 小瓶 | |
| 进价(元/瓶) | 5 | 2 |
| 售价(元/瓶) | 7 | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com