
【题目】在梯形ABCD中,AD∥BC , AB=CD , ∠AOD=60°,E为OA的中点,F为OB的中点,G为CD的中点,试判断△EFG的形状并说明理由 . 
【答案】解:△EFG为等边三角形;证明如下:
如图,连接DE、CF;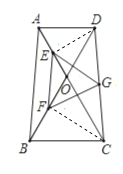
∵AD∥BC , AB=CD ,
∴四边形ABCD为等腰梯形,
∴AC=BD;
在△ABD与△DCA中,
AB=DC
AD=DA
BD=AC
∴△ABD≌△DCA(SSS),
∴∠OAD=∠ODA , AO=DO;而∠AOD=60°,
∴△AOD为等边三角形,AD=OD;
∵AE=OE ,
∴DE⊥AO , △CDE为直角三角形,
∵DG=CG ,
∴EG= ![]() CD;同理可求:FG=
CD;同理可求:FG= ![]() CD;
CD;
∵E为OA的中点,F为OB的中点,
∴EF为△OAB的中位线,
∴EF= ![]() AB;而AB=CD ,
AB;而AB=CD ,
∴EG=FG=EF ,
∴△EFG为等边三角形 .
【解析】如图,作辅助线;首先证明∠OAD=∠ODA , 得到AO=DO , 结合∠AOD=60°,判断出△AOD为等边三角形,此为解题的关键性结论;其次证明DE⊥AC , 运用直角三角形的性质证明EG=FG= ![]() CD;运用三角形的中位线定理证明EF=
CD;运用三角形的中位线定理证明EF= ![]() AB , 结合AB=CD , 得到EG=FG=EF , 即可解决问题 .
AB , 结合AB=CD , 得到EG=FG=EF , 即可解决问题 .
【考点精析】利用三角形中位线定理对题目进行判断即可得到答案,需要熟知连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:初中数学 来源: 题型:
【题目】若a,b,c是直角三角形的三条边长(c为斜边长),斜边上的高是h,给出下列结论:
①长为a2,b2,c2的三条线段能组成一个三角形;②长为![]() ,
,![]() ,
,![]() 的三条线段能组成一个三角形;③长为a+b,c+h,h的三条线段能组成直角三角形;④长为
的三条线段能组成一个三角形;③长为a+b,c+h,h的三条线段能组成直角三角形;④长为![]() ,
,![]() ,
,![]() 的三条线段能组成直角三角形.
的三条线段能组成直角三角形.
其中所有正确结论的序号为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图:直线AB⊥BC,四边形ABCD是正方形,且AB=6,点P是BD上一点,且PD=2![]() ,一块三角板的直角顶点放在点P上,另两条边与BC、AB所在直线相交于点E、F,在三角板绕点P旋转的过程中,使得△PBF是等腰三角形,(1)线段BD=________,(2)请写出所有满足条件的BF的长__________.
,一块三角板的直角顶点放在点P上,另两条边与BC、AB所在直线相交于点E、F,在三角板绕点P旋转的过程中,使得△PBF是等腰三角形,(1)线段BD=________,(2)请写出所有满足条件的BF的长__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在△ABC中三个内角的度数满足∠ABC:∠C:∠A=5:6:7,BD是△ABC的角平分线,DE是△DBC的高.
(1)求△ABC各内角的度数;
(2)求图中的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若AC=5,BC=3,则BD的长为( )

A. 1 B. ![]() C.
C. ![]() D. 4
D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题,真命题是( ) 
A.如图,如果OP平分∠AOB,那么,PA=PB
B.三角形的一个外角大于它的一个内角
C.如果两条直线没有公共点,那么这两条直线互相平行
D.有一组邻边相等的矩形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+x﹣6与x轴两个交点分别是A、B(点A在点B的左侧). 
(1)求A、B的坐标;
(2)利用函数图象,写出y<0时,x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com