
 如图,AB∥CD,若∠1=35°,则∠2的度数为145°.
如图,AB∥CD,若∠1=35°,则∠2的度数为145°.  金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
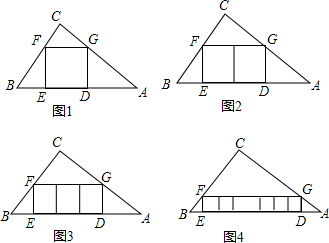
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
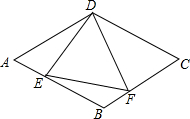 如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.
如图,菱形ABCD中,AB=6,∠A=60°,点E是线段AB上一点(不与A,B重合),作∠EDF交BC于点F,且∠EDF=60°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
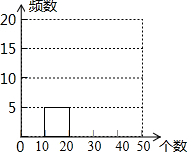 体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.
体育课的一个项目是排球30秒对墙垫球,为了解某校七年级学生此项目平时的训练情况,随机抽取了该校部分七年级学生进行测试,根据测试结果,制作了如下尚不完整的频数分布表,其中第1组垫球个数在10≤x<20的人数占被调查人数的10%.| 组别 | 垫球个数x(个) | 频数(人数) |
| 1 | 10≤x<20 | 5 |
| 2 | 20≤x<30 | a |
| 3 | 30≤x<40 | 20 |
| 4 | 40≤x<50 | 16 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com