
【题目】在△ABC中,∠BAC=45°,CD⊥AB于点D,AE⊥BC于点E,连接DE.
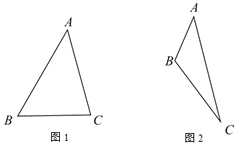
(1)如图1,当△ABC为锐角三角形时,
①依题意补全图形,猜想∠BAE与∠BCD之间的数量关系并证明;
②用等式表示线段AE,CE,DE的数量关系,并证明;
(2)如图2,当∠ABC为钝角时,依题意补全图形并直接写出线段AE,CE,DE的数量关系.
【答案】(1)①补全图形,如图1所示.见解析;猜想:∠BAE=∠BCD. 理由见解析;②见解析;(2)补全图形,如图3所示. 见解析;线段AE,CE,DE的数量关系:CE-![]() DE=AE.
DE=AE.
【解析】
(1)①依题意补全图形,由直角三角形的性质得出∠BAE﹢∠B=90°,
∠BCD﹢∠B=90°即可得出∠BAE=∠BCD;
②在AE上截取AF=CE,可证出△ACD是等腰直角三角形,得出AD=CD,可证明△ADF≌△CDE,得出DF=DE, ∠ADF=∠CDE,可推出∠CDE﹢∠FDC=∠EDF=90°.证出△EDF是等腰直角三角形,得出EF=![]() ,即可得出结论;
,即可得出结论;
(2) 在CE上截取CF=AE,连接DF由CD⊥AD,AE⊥BC,可得∠EAD=∠DCF
由∠BAC=45°可得AD=CD,可证△ADE≌△CDF,可得ED=DF∠ADE=∠CDF,可推出∠EDF=90°可得△EDF是等腰直角三角形故![]() ,即可得线段AE,CE,DE的数量关系.
,即可得线段AE,CE,DE的数量关系.
(1)①依题意,补全图形,如图1所示.

猜想:∠BAE=∠BCD.
理由如下:
∵CD⊥AB,AE⊥BC,
∴∠BAE﹢∠B=90°,
∠BCD﹢∠B=90°.
∴∠BAE=∠BCD.
②证明:如图2,在AE上截取AF=CE.

连接DF.
∵∠BAC=45°,CD⊥AB,
∴△ACD是等腰直角三角形.
∴AD=CD.
又∠BAE=∠BCD,
∴△ADF≌△CDE(SAS).
∴DF=DE, ∠ADF=∠CDE.
∵AB⊥CD,
∴∠ADF﹢∠FDC=90°.
∴∠CDE﹢∠FDC=∠EDF=90°.
∴△EDF是等腰直角三角形.
∴EF=![]() .
.
∵AF+EF=AE,
∴CE+![]() DE=AE.
DE=AE.
(2)依题意补全图形,如图3所示.

在CE上截取CF=AE,连接DF
∵CD⊥AD,AE⊥BC
∴∠ADC=∠AEC=90°
∴∠EAB+∠ABE=90°,∠DBC+∠DCF=90°,∠ABE=∠CBD
∴∠EAD=∠DCF
∵∠BAC=45°
∴∠DCA=45°
∴AD=CD
又∵CF=AE
∴△ADE≌△CDF
∴ED=DF
∠ADE=∠CDF
∵∠CDF+∠ADF=90°
∴∠ADE+∠ADF=90°
∴∠EDF=90°
∴△EDF是等腰直角三角形
∴![]()
∵CE=CF+EF
∴![]()
∴线段AE,CE,DE的数量关系:CE-![]() DE=AE.
DE=AE.
故答案为:CE-![]() DE=AE
DE=AE


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
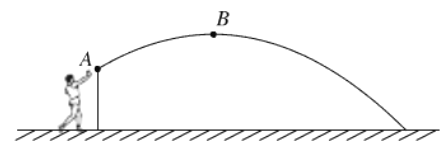
【题目】为了在校运会中取得更好的成绩,小丁积极训练.在某次试投中铅球所经过的路线是如图所示的抛物线的一部分.已知铅球出手处A距离地面的高度是![]() 米,当铅球运行的水平距离为3米时,达到最大高度
米,当铅球运行的水平距离为3米时,达到最大高度![]() 的B处.小丁此次投掷的成绩是多少米?
的B处.小丁此次投掷的成绩是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2﹣2x+3
(1)求出顶点,并画出二次函数的图象.
(2)根据图象解决下列问题
①若y>0,写出x的取值范围.
②求出﹣![]() ≤x≤2时,y的最大值和最小值.
≤x≤2时,y的最大值和最小值.
③求出﹣5<y<3时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某公司要建一个矩形的产品展示台,展示台的一边靠找为9m的宣传版(这条边不能超出宣传版),另三边用总长为40m的红布粘贴在展示台边上.设垂直于宣传版的一边长为![]()
(1)当展示台的面积为128m2时,求![]() 的值;
的值;
(2)设展示台的面积为![]() ,求
,求![]() 的最大值.
的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,反比例函数![]() 的图象和
的图象和![]() 都在第一象限内,
都在第一象限内,![]() ,
,![]() 轴,且
轴,且![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
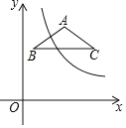
(1)若反比例函数![]() 的图象经过点B,求此反比例函数的解析式;
的图象经过点B,求此反比例函数的解析式;
(2)若将![]() 向下平移
向下平移![]() (m>0)个单位长度,
(m>0)个单位长度,![]() ,
,![]() 两点的对应点同时落在反比例函数图象上,求
两点的对应点同时落在反比例函数图象上,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=﹣x2+(m﹣1)x+m的对称轴为x=![]() ,请你解答下列问题:
,请你解答下列问题:
(1)m= ,抛物线与x轴的交点为 .
(2)x取什么值时,y的值随x的增大而减小?
(3)x取什么值时,y<0?
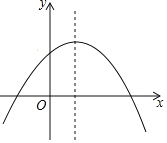
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O直径,半径OC⊥AB,连接AC,∠CAB的平分线AD分别交OC于点E,交![]() 于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )
于点D,连接CD、OD,以下三个结论:①AC∥OD;②AC=2CD;③线段CD是CE与CO的比例中项,其中所有正确结论的序号是( )

A.①②B.②③
C.①③D.①②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形![]() 的两个顶点
的两个顶点![]() ,
,![]() 在反比例函数
在反比例函数![]() 的图象上,对角线
的图象上,对角线![]() 与
与![]() 的交点恰好是坐标原点
的交点恰好是坐标原点![]() ,已知点
,已知点![]() ,
,![]() .
.

(1)求反比例函数的解析式;
(2)点![]() 是
是![]() 轴上一点,若
轴上一点,若![]() 是等腰三角形,直接写出点
是等腰三角形,直接写出点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,△ABC的三个顶点坐标分别为A(1,1),B(4,0),C(4,4).
(1)按下列要求作图:
①将△ABC向左平移4个单位,得到△A1B1C1;
②将△A1B1C1绕点B1逆时针旋转90°,得到△A2B2C2.
(2)求点C1在旋转过程中所经过的路径长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com