
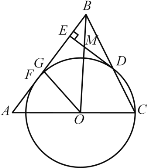
【题目】如图,在△ABC中,AB=AC=10,tan∠A=![]() ,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
(1)求证:DE是⊙O的切线;
(2)当⊙O与AB相切于点F时,求⊙O的半径;
(3)在(2)的条件下,连接OB交DE于点M,点G在线段EF上,连接GO.若∠GOM=45°,求DM和FG的长.
【答案】(1)见解析;(2)r=![]() ;(3)DM=
;(3)DM=![]() ,FG=
,FG=![]()
【解析】
(1)连接OD,根据等腰三角形判断出∠ABC=∠ACB,进而得到OD∥AB即可得到求证;
(2)连接OF,根据切线得到△AOF是直角三角形,根据tan∠A=![]() ,设半径OF=OC=r,则可表示出AF=
,设半径OF=OC=r,则可表示出AF=![]() r,AO=10-r,勾股定理求出半径即可得到结果;
r,AO=10-r,勾股定理求出半径即可得到结果;
(3)现根据题意证出ODEF是正方形,求出BE,再根据△BEM∽△ODM,即可得到MD;在EF延长线上截取FT=DM,证明出OT=OM,再证明△OGT≌△OGM,则GM=GT=GF+FT=GF+DM,设出GF=a,根据勾股定理求解即可.
解:(1)证明:连接OD
∵OC,OD均为⊙O的半径,
∴OC=OD,
∴∠DCO=∠CDO
又∵在△ABC中,AB=AC,
∴∠ABC=∠ACB
∴∠ABC=∠CDO,
∴OD∥AB
∵DE⊥AB,
∴DE⊥OD
∴DE是⊙O的切线.
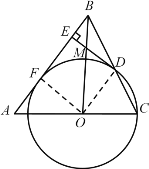
(2)解:连接OF,设⊙O的半径为r,则OF=r,OC=r
∵⊙O与AB相切于点F,
∴AB⊥OF,
∴∠OFA=90°,
在Rt△AOF中,∠OFA=90°,OF=r,tan∠A=![]()
∴AF=![]() r,
r,
∴AO=![]() r
r
又∵AO=AC-OC=10-r,
∴![]() r=10-r
r=10-r
∴ r=![]() .
.
(3)由(2)知r= ![]() ,
,
∴AF=![]() r=
r=![]()
∵∠ODE=∠DEF=∠OFE=90°,
∴四边形ODEF是矩形
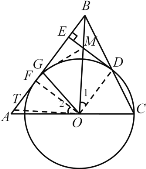
∵OF=OD,
∴矩形ODEF是正方形,
∴DE=EF=OF= ![]()
∴BE=AB-AF-EF=10-![]() -
-![]() =
=![]()
∵∠BME=∠OMD,∠BEM=∠ODM=90°
∴△BEM∽△ODM,
∴![]()
即  =
= ![]() ,解得DM=
,解得DM=![]()
在EF延长线上截取FT=DM
∵四边形ODEF是正方形,
∴∠OFT=∠ODM=90°,OF=OD
∴△OFT≌△ODM,
∴∠2=∠1,OT=OM
∵∠DOF=90°,∠GOM=45°,
∴∠GOF+∠1=45°,
∴∠GOF+∠2=45°
即∠GOT=45°,
∴∠GOT=∠GOM
又OG=OG,
∴△OGT≌△OGM,
∴GM=GT=GF+FT=GF+DM
设GF=a,则EG= ![]() -a,GM=
-a,GM= ![]() +a,且EM=DE-DM=
+a,且EM=DE-DM=![]() -
-![]() =
= ![]()
在Rt△EMG中,EM 2+EG 2=GM 2,即(![]() )2+(
)2+(![]() -a )2=(
-a )2=(![]() +a )2,解得a=
+a )2,解得a=![]()
∴FG的长为![]() .
.


科目:初中数学 来源: 题型:
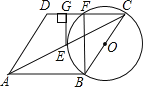
【题目】如图,以ABCD的边BC为直径的⊙O交对角线AC于点E,交CD于点F.连结BF.过点E作EG⊥CD于点G,EG是⊙O的切线.
(1)求证:ABCD是菱形;
(2)已知EG=2,DG=1.求CF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 和抛物线
和抛物线![]() :
:![]() ,其中
,其中![]() .
.
![]() 下列说法你认为正确的序号是______;
下列说法你认为正确的序号是______;
![]() 抛物线
抛物线![]() 和
和![]() 与y轴交于同一点
与y轴交于同一点![]() ;
;
![]() 抛物线
抛物线![]() 和
和![]() 开口都向上;
开口都向上;
![]() 抛物线
抛物线![]() 和
和![]() 的对称轴是同一条直线;
的对称轴是同一条直线;
![]() 当
当![]() 时,抛物线
时,抛物线![]() 和
和![]() 都与x轴有两个交点
都与x轴有两个交点
![]() 抛物线
抛物线![]() 和
和![]() 相交于点E、F,当k的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
相交于点E、F,当k的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
![]() 在
在![]() 中,若抛物线
中,若抛物线![]() 的顶点为M,抛物线
的顶点为M,抛物线![]() 的顶点为N,问:
的顶点为N,问:
是否存在实数k,使![]() ?如存在,求出实数k;如不存在,请说明理由.
?如存在,求出实数k;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ABC中,∠C=90°,∠A≠∠B.
(1)请利用直尺和圆规作出△ABC关于直线AC对称的△AGC;(不要求写作法,保留作图痕迹)
(2)在AG边上找一点D,使得BD的中点E满足CE=AD.请利用直尺和圆规作出点D和点E;(不要求写作法,保留作图痕迹)
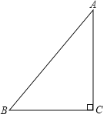
查看答案和解析>>
科目:初中数学 来源: 题型:
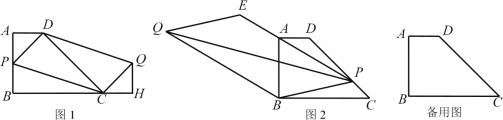
【题目】已知在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=4,BC=6.
(1)如图1,P为AB边上一点,以PD,PC为边作平行四边形PCQD,过点Q作QH⊥BC,交BC的延长线于H.求证:△ADP≌△HCQ;
(2)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE.请问对角线PQ的长是否存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
(3)如图2,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE,PB为边作平行四边形PBQE.请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,∠B=36°,AD是斜边BC上的中线,将△ACD沿AD折叠,使点C落在点F处,线段DF与AB相交于点E.
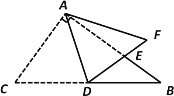
(1)求∠BDE的度数.
(2)求证:△DEB∽△ADB.
(3)若BC=4,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
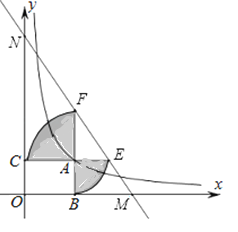
【题目】如图,已知动点A在函数![]() 的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA交以A为圆心AB长为半径的圆弧于点E,延长BA交以A为圆心AC长为半径的圆弧于点F,直线EF分别交x轴、y轴于点M、N,当NF=4EM时,图中阴影部分的面积等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB和抛物线的交点是A(0,-3),B(5,9),已知抛物线的顶点D的横坐标是2.
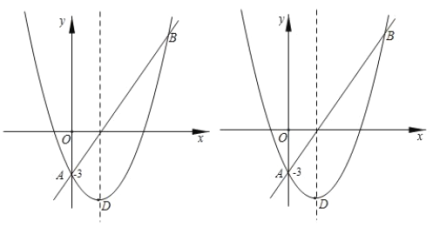
(1)求抛物线的解析式及顶点坐标;
(2)在![]() 轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
轴上是否存在一点C,与A,B组成等腰三角形?若存在,求出点C的坐标,若不存在,请说明理由;
(3)在直线AB的下方抛物线上找一点P,连接PA,PB使得△PAB的面积最大,并求出这个最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 交
交![]() 轴于点
轴于点![]() 、
、![]() ,交
,交![]() 轴于点
轴于点![]() ,在
,在![]() 轴上有一点
轴上有一点![]() ,连接
,连接![]() .
.

(1)求二次函数的表达式;
(2)若点![]() 为抛物线在
为抛物线在![]() 轴负半轴上方的一个动点,求
轴负半轴上方的一个动点,求![]() 面积的最大值;
面积的最大值;
(3)抛物线对称轴上是否存在点![]() ,使
,使![]() 为等腰三角形,若存在,请直接写出所有
为等腰三角形,若存在,请直接写出所有![]() 点的坐标,若不存在请说明理由.
点的坐标,若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com