


科目:初中数学 来源: 题型:
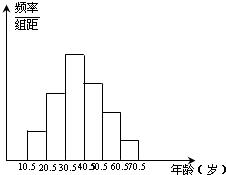 (2004•龙岩)今年4月25日,我市举行龙岩冠豸山机场首航仪式,利用这一契机,推出“冠豸山绿色之旅”等多项旅游项目.“五•一”这天,对连城八家旅行社中部分游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成频率分布直方图(如图示).已知从左到右依次为1~6小组的频率分别是0.08、0.20、0.32、0.24、0.12、0.04,第1小组的频数为8,请结合图形回答下列问题:
(2004•龙岩)今年4月25日,我市举行龙岩冠豸山机场首航仪式,利用这一契机,推出“冠豸山绿色之旅”等多项旅游项目.“五•一”这天,对连城八家旅行社中部分游客的年龄(年龄取整数)进行了抽样统计,经整理后分成六组,并绘制成频率分布直方图(如图示).已知从左到右依次为1~6小组的频率分别是0.08、0.20、0.32、0.24、0.12、0.04,第1小组的频数为8,请结合图形回答下列问题:查看答案和解析>>
科目:初中数学 来源:2004年全国中考数学试题汇编《二次函数》(05)(解析版) 题型:解答题
 x2+
x2+ x+3与x轴交于点A、B两点,过定点的直线l:y=
x+3与x轴交于点A、B两点,过定点的直线l:y=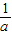 x-2(a≠0)交x轴于点Q.
x-2(a≠0)交x轴于点Q.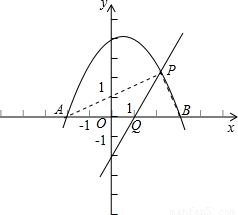
查看答案和解析>>
科目:初中数学 来源:2004年福建省龙岩市中考数学试卷(解析版) 题型:解答题
 x2+
x2+ x+3与x轴交于点A、B两点,过定点的直线l:y=
x+3与x轴交于点A、B两点,过定点的直线l:y=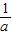 x-2(a≠0)交x轴于点Q.
x-2(a≠0)交x轴于点Q.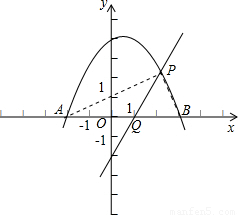
查看答案和解析>>
科目:初中数学 来源:2004年福建省龙岩市中考数学试卷(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com