
分析 (1)根据题意求出m,解方程组求出M点坐标,根据二次函数的性质求出p、q,得到二次函数的解析式;
(2)根据一元二次方程根的判别式进行判断;
(3)根据二次函数的性质求出点C的坐标、点A的坐标,根据勾股定理求出CM,根据勾股定理的逆定理判断△CMA是直角三角形,根据三角形的外接圆的性质计算.
解答 解:(1)把D(0,-3)坐标代入直线y=x+m中,
得m=-3,从而得直线y=x-3,
由M为直线y=-$\frac{1}{2}x$与直线y=x-3的交点,
得$\left\{\begin{array}{l}y=-\frac{1}{2}x\\ y=x-3\end{array}\right.$,
解得,$\left\{\begin{array}{l}x=2\\ y=-1\end{array}\right.$,
∴得M点坐标为M(2,-1),
∵M为二次函数y=x2+px+q的顶点,
∴其对称轴为x=2,
由对称轴公式:x=-$\frac{b}{2a}$,得-$\frac{p}{2}$=2,
∴p=-4;
由$\frac{{4ac-{b^2}}}{4a}$=-1,
$\frac{{4q-{{(-4)}^2}}}{4}$=-1,
解得,q=3.
∴二次函数y=x2+px+q的解析式为:y=x2-4x+3;
(2)∵M是直线y=-$\frac{1}{2}x$和y=x+m的交点,
∴$\left\{\begin{array}{l}y=-\frac{1}{2}x\\ y=x+m\end{array}\right.$,
解得,$\left\{\begin{array}{l}x=-\frac{2}{3}m\\ y=\frac{1}{3}m\end{array}\right.$,
∴M点坐标为M(-$\frac{2}{3}m$,$\frac{1}{3}m$),
∴-$\frac{p}{2}$=-$\frac{2}{3}m$、$\frac{{4q-{{(\frac{4}{3}m)}^2}}}{4}$=$\frac{1}{3}m$,
解得,p=$\frac{4}{3}m$,q=$\frac{4}{9}{m^2}$+$\frac{1}{3}m$,
由$\left\{\begin{array}{l}y=x+m\\ y={x^2}+px+q\end{array}\right.$,得x2+(p-1)x+q-m=0,
△=(p-1)2-4(q-m)
=($\frac{4}{3}m$-1)2-4($\frac{4}{9}{m^2}$+$\frac{1}{3}m$-m)=1>0,
∴二次函数y=x2+px+q的图象与直线y=x+m总有两个不同的交点;
(3)由(1)知,二次函数的解析式为:y=x2-4x+3,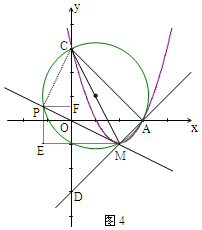
当x=0时,y=3.
∴点C的坐标为C(0,3),
令y=0,即x2-4x+3=0,
解得x1=1,x2=3,
∴点A的坐标为A(3,0),
由勾股定理,得AC=3$\sqrt{2}$.
∵M点的坐标为M(2,-1),
过M点作x轴的垂线,垂足的坐标应为(2,0),
由勾股定理得,AM=$\sqrt{2}$,
过M点作y轴的垂线,垂足的坐标应为(0,-1),
由勾股定理,得CM=$\sqrt{{4^2}+{2^2}}$=$\sqrt{20}$=2$\sqrt{5}$.
∵AC2+AM2=20=CM2,
∴△CMA是直角三角形,
CM为斜边,∠CAM=90°.
直线y=-$\frac{1}{2}x$与△CMA的外接圆的一个交点为M,另一个交点为P,
则∠CPM=90°.即△CPM为Rt△,
设P点的横坐标为x,则P(x,-$\frac{1}{2}x$).过点P作x轴垂线,
过点M作y轴垂线,两条垂线交于点E,则E(x,-1).
过P作PF⊥y轴于点F,则F(0,-$\frac{1}{2}x$).
在Rt△PEM中,PM2=PE2+EM2
=(-$\frac{1}{2}x$+1)2+(2-x)2=$\frac{5}{4}{x^2}$-5x+5.
在Rt△PCF中,PC2=PF2+CF2=x2+(3+$\frac{1}{2}x$)2
=$\frac{5}{4}{x^2}$+3x+9.
在Rt△PCM中,PC2+PM2=CM2,
得$\frac{5}{4}{x^2}$+3x+9+$\frac{5}{4}{x^2}$-5x+5=20,
化简整理得5x2-4x-12=0,
解得x1=2,x2=-$\frac{6}{5}$.
当x=2时,y=-1,即为M点的横、纵坐标.
∴P点的横坐标为-$\frac{6}{5}$,纵坐标为$\frac{3}{5}$,
∴P(-$\frac{6}{5}$,$\frac{3}{5}$).
点评 本题考查的是二次函数知识的综合运用,掌握二次函数的性质、一元二次方程根的判别式是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
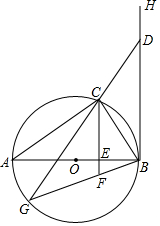 已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4$\sqrt{3}$.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.
已知:AB为⊙O的直径,C是⊙O上一点,如图,AB=12,BC=4$\sqrt{3}$.BH与⊙O相切于点B,过点C作BH的平行线交AB于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
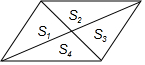 如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )
如图,平行四边形的两条对角线将平行四边形的面积分成四部分,分别记作S1,S2,S3,S4,下列关系式成立的是( )| A. | S1<S2<S3<S4 | B. | S1=S2=S3=S4 | C. | S1+S2>S3+S4 | D. | S1=S3<S2=S4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
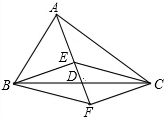 如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是②(只填写序号).
如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF,给出下列条件:①BE⊥EC;②AB=AC;③BF∥EC;从中选择一个条件使四边形BECF是菱形,你认为这个条件是②(只填写序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com